The Problem(s) with the Standard Cosmological Model

I have talked quite a bit in recent posts about the FUGE model which I see as the simplest model that results in a universe that looks like ours, given certain parameters.

The alternative, the standard cosmological model, which involves a short period of “standard” expansion, then inflation, then two periods of deceleration and finally the current acceleratory period, is fiendishly complicated.

To illustrate, I have put together some graphs that show a comparison between the FUGE model and the standard cosmological model.

There are some assumptions that I have had to make, and I will try to specify them comprehensively here because there are varying assumptions made under the umbrella of the standard cosmological model.  First, however, there are the two (yes, only two) assumptions for the FUGE model, which are that:

• for every unit of Planck time, the radius of the universe increases by one unit of Planck length, and
• for every unit of Planck time, the mass-energy in the universe increases by half a unit of Planck mass.

The assumptions made (by me) about the standard cosmological model are that:

• the density today is equal to the critical density (NASA)
• the radius of the total universe is currently 46.5 billion light years – where this is the minimum size, based on calculations of comoving distance to where the cosmic microwave background originated (wikipedia but also SCSU and UCLA)
• the total mass of ordinary and dark matter is invariant – that is both have been in the universe since before the inflationary period and the total combined mass does not change (Ethan Siegel)
• the density of dark energy is invariant (Ethan Siegel)
• the distribution of ordinary matter, dark matter and dark energy is 4.6%, 24.0% and 71.4% (WMAP)
• critical density is given by ρ_c=3H²/8πG (wikipedia)
• prior to the inflationary period the universe expanded at the speed of light (with an equation of state value of w=-1/3)
• the inflationary period was between t=10^-36 to t=10^-32s (wikipedia), expanding the universe by a factor of 10²⁶ (wikipedia), at a rate that peaked midway (at about t= t=5×10^-33s), the graphs show an notional acceleration and deceleration to achieve the decelerated rate of expansion from t=10^-32s onwards
• during the radiation-dominated era which extended to 47,000 years (wikipedia), the equation of state value was w=1/3
• during the matter-dominated era which extended from 47,000 years to about 9.8 billion years (wikipedia), the equation of state value was w=0, and
• during the current inflationary era, the dark-energy-dominated era (wikipedia), the equation of state value is w=-1.03 (Planck collaboration - via wikipedia).

Note that all the graphs below extend from when the universe was one unit of Planck time old to 328 billion light years and they are in logarithmic scale (on both axes).  Age of the universe is given in seconds.  The right extent brings us to when the Big Rip has started (assuming accelerated expansion at w=-1.03).  The left extent eliminates the need to illustrate a potential infinite density at t=0.  Personally, I don’t think there was ever infinite density*.

The first shows how the radius of the universe has evolved over time.  To emphasise, I have compared the radius to the age of the universe multiplied by the speed of light:

The next shows the quantity of mass-energy, expressed in terms of mass.  To emphasise, I have compared the mass-energy to the age of the universe (in units of Planck time) multiplied by half a unit of Planck mass.  I have zoomed in, eliminating the upper half of the straight line for the standard cosmological model in order to highlight the kink that kicks in during the dark-energy-dominated era.  This should not surprise, because this is the “dark-energy-dominated era”, however the timing of that upward spike should be surprising – right now.  This is, however, just an artefact of the graph.  That bend happens at 9.8 billion years, and there’s very little difference between log₁₀ of 9.8 billion and 13.7 billion (about 2%):

Third is mass-energy density, again expressed in terms of mass density.  To emphasise, I have compared the density to critical density (as it changes over time).

Note that universe has, in the standard cosmological model, had a critical density three times – briefly during the inflationary era, again briefly about one ten thousandths of a second and … right now.

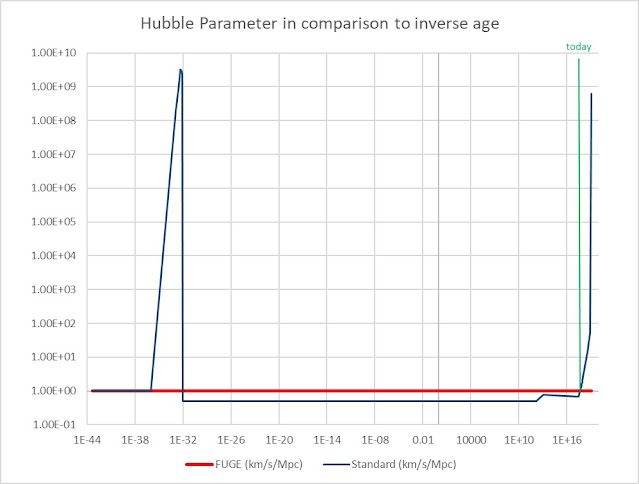
Finally, the Hubble parameter expressed in kilometres per second per megaparsec.  To emphasis, I have compared the Hubble parameter to the inverse of the age of the universe (when expressed in kilometres per second per megaparsec):

Note that the Hubble parameter was equal to the inverse age of the universe three times.  From the beginning until just prior to the inflationary era, at the end of the inflationary era and … right now.

Those standard cosmological model curves are some real crazy shit.  And the assumptions required … well, let’s just say I have my reservations about those too.

---

* Even before the FUGE model, I suspected that initial packing of the universe’s mass-energy would have been the equivalent of one unit of Planck mass per Planck volume (notionally a sphere with radius of one unit of Planck length).  I thought that this would have been incredibly hot and unstable, trying desperately to expand while being held in a vice-like grip by gravity (since it was much denser than a black hole of equivalent mass-energy).  When a rupture opened up, I imagined that the universe would have flipped inside out, leading to space expanding rapidly, with the unleashed mass-energy on its tail (figuratively, of course) – and thus the Big Bang.  I no longer think that this is viable, since that density would have been hugely more than that of a non-rotating black hole of the same mass.