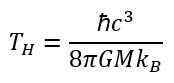No, Espen Haug, You Cannot Just Magic God Time out of Empty Space

I recently wrote about Eugene Tatum’s assertion that the CMB is related to the Hawking Temperature of the universe.  The coauthor of that particular paper was Espen Gaarder Haug.  I didn’t mention it before, but Tatum is a Doctor, of Anatomic and Clinical Pathology.  Haug is also a Doctor, in the area of finance, specifically quantitative finance.  He got his doctorate in something relevant to options and trading (his doctoral thesis was on that anyway) but I can’t find out what he did his undergraduate in (presumably economics, but not necessarily).  He’s currently a finance professor at the Norwegian University of Life Sciences.

Haug and Tatum are coauthors on a range of papers about the flat cosmological model (which they sometimes refer to as the Haug-Tatum cosmology [HTC] model), while Haug has a quite a few papers of his own about the quantisation of gravity.

During research for No Eugene Tatum, Hawking Temperature is not Related to CMB, I stumbled upon one of Haug’s paper on the quantisation of gravity: God Time = Planck Time: Finally Detected! And Its Relation to Hubble Time.  Note that, like most of Haug’s papers, this one was published at scirp.org, which is a predatory publisher.  That said, being published in an odd place does not necessarily make the content wrong.  It’s just easier to get such publishers to publish bad and low-quality science – and even easier to publish at a blog under a pseudonym.  When you find a paper published by a pay-to-play or predatory publisher, you just need to be more careful and engage your critical thinking more intently than you might otherwise, such as when the source is more reputable.

The very first thing drew my attention was the title.  “God time”?  I wondered if I was looking at the work of someone like Luke Barnes, a person dabbling in physics to support a theological world view.  On closer inspection, and in the context of Haug’s other papers, including two others that mention “god”, it appears that he is just using a hook to draw attention rather than making any serious claim about the existence of an actual god.  Haug does refer to the “the god particle” in at least two of his papers without mentioning that the Higgs boson was know as the “god-damned particle” due to its reticence to reveal itself, which is unfortunate but, in the conclusion to the God Time paper, he indicates that historical references to indivisibility at the smallest scales, including apparent biblical references, are not important.

The basic claim of the God Time paper, and the one that I have a problem with, is that knowledge of G, ħ, and c is unnecessary to establish the value of t_P, the Planck time.  (In another paper, and another, Haug seems most intent on removing the use of G entirely, which is odd.  There are problems in those papers too, but I will try to restrict my efforts here to addressing Haug’s efforts to eliminate fundamental constants.)

---

The standard definition of Planck time is:

Given that the defined value consists of G, ħ, and c, and only G, ħ, and c, establishing Planck time without the use of those fundamental constants should be quite a challenge.  Haug does it by using the equation:

Which he later generalises (in a special case) to:

In his numerical example for the first equation, Haug sets object 1 to the Sun and object 2 to the Earth.  The term δ is used to refer to the effect of  gravitational lensing by object 1 (the Sun), expressed in radians.  (Note that in the link provided, the symbol θ is used.) The term g refers to the magnitude of gravitational acceleration at object 2 (the Earth).  Note that the equation at the link has a direction that is implied by the minus sign, it’s not intended to refer to a negative value.  The term λ is a reference to the Compton wavelength of the mass of the relevant object, but in this case it is the reduced variant, in the same way that the reduced Planck constant is given by ħ=h/2π.  So, for clarity, Haug provides the numerical result for this equation (using subscripts E for Earth and S for Sun):

where (per the links above)

If we substitute these into Haug’s equation, we get:

which resolves to

In his generalised version, Haug is talking about a single mass, so no subscripts are required, and:

which also resolves to

So, yes, you can get Planck time using Haug’s equation which does not explicitly use G, ħ and c.  However, there is a problem with his assertion that we can therefore reach a value for Planck time without using any of the fundamental constants because, in order to use his method, we must establish the values for at least gravitational lensing deflection and the reduced Compton wavelength.

The value for gravitational lensing deflection due to the Sun has been measured, first by Eddington in 1919, so while not so easy, this is entirely possible – with some caveats.  The apparent radius r in the equation (per Wikipedia), θ=4GM/c²r, is not necessarily the radius of the body with the mass M, but rather the distance between the centre of the mass and the radiation being deflected.  The value measured by Eddington was for light that grazed the surface of the sun, hence the need to observe a total solar eclipse.  The related deflection is, therefore, at the photosphere, which is considered be the surface of the sun, and r=R_s.

The Compton wavelength, on the other hand, is not something that is measured for, and probably doesn’t even apply to, bodies at the scale of the Earth and the Sun (because it’s a quantum mechanical property).  We can calculate it, sure, but to do so we need to use both ħ and c.  (This could explain Haug’s fixation on eliminating G in his other papers, if he has noted that he can’t get around using ħ and c.  He says it explicitly in section 6 of another paper.)

If we forgive this, then we still have some problems to address.  The accuracy of the value of t_P that can be determined using Haug’s first equation depends on the accuracy of the measurement of:

Deflection due to gravity as light grazes the surface of the sun – 3%

Gravitational acceleration at some point on the Earth with a distance from the centre of R_E (not the defined standard gravity value which is nominal and limited by caveats) – about 0.7% assuming it’s somewhere on the surface

The distance to the centre of the Earth used above (about ±30mm in 6378km) – 0.0000005%

The radius of the photosphere – 0.02%

The mass of the Sun (for calculating the reduced Compton wavelength) – 0.005%

The mass of the Earth (ditto)– 0.01%

We don’t need to worry about the accuracy of h and c, because these values are both defined.  The only inaccuracy in ħ will be due to the approximation to π that is used, but this can be set arbitrarily low by using π to many significant numbers.  So this means the resultant inaccuracy in the measurement of t_P would be, approximately:

3%+(0.7%/2)+0.02%+0.005%+0.0000005%+(0.01%/2)=3.38%

Presumably, from a value of t_P determined this way, we could calculate a value for G using the standard definition of t_P and the defined values of ħ and c.  This value would have an accuracy of approximately 6.76%.

Compare this with the NIST values which have accuracies of 0.0011% for t_P and 0.0022% for G.

---

As indicated above, Haug seems to realise that he can’t get around using ħ and c, and is therefore laser focussed on eliminating the use of G, even in the process of determining the value of t_P.

This, to me, is madness.  If expressed in Planck units, all the four values listed above, ħ, c, G and t_P, resolve to unity.  (In addition, m_P, l_P, q_P, v_P, i_P, T_P, E_P, k_B, k_e, m_P, reduced μ₀ and raised ε₀ also resolve to unity.  Even the unitless gravitational and electromagnetic coupling constants resolve to unity when Planck values for mass and charge are used as the reference rather than arbitrary values like a proton or electron mass or the elementary charge.)

---

In other papers, like Quantum Gravitational Energy Simplifies Gravitational Physics and Gives a New Einstein Inspired Quantum Field Equation without G and Not Relying on the Newton Gravitational Constant Gives More Accurate Gravitational Predictions, Haug suggests that he’s hit upon some evidence of the quantisation of gravity – all which seem to relate to the notions of “collision length” and “collision time” (which is expanded on in Collision-space-time: Unified quantum gravity – where he assigns photons with a mass (an extremely tiny mass, admittedly)).

In the first two papers above, Haug mentions the “factor”:

Which he refers to as “reduced Compton frequency per Planck time”.  This is an odd way of putting it, for more than one reason.  First, as a simile, we could say that Gm_P²/ħ is “Planck length per Planck time”.  This not completely untrue, because Gm_P²/ħ=c=l_P/t_P, but it’s an odd way of putting it.  The second reason may not be immediately clear, but we can look at Haug’s own words, from Quantum Gravitational Energy Simplifies Gravitational Physics and Gives a New Einstein Inspired Quantum Field Equation without G:

It's not anything “per Planck time”, it’s a value that is multiplied by Planck time, not divided.  If anything, it’s equivalent to “Planck time per reduced Compton period”, noting that there’s another error buried in there.

Haug states that the reduced Compton frequency is the speed of light divided by the reduced Compton wavelength.  Presumably, the vanilla Compton frequency (f_c) is the speed of light (c) divided by the vanilla Compton wavelength (λ_c):

If we implement the reduced Compton wavelength, which is the Compton wavelength divided by 2π, we have (using the bar as an indication of some sort of modification, not necessarily reduction):

So it’s not a reduced Compton frequency, it’s a raised Compton frequency.

He could, however, express things somewhat less awkwardly.  Using the definitions of reduced Compton wavelength and Planck length, we see that:

And, in flat universe, we know that*:

So, Haug’s “factor” is, in fact, simply an expression for the age of the universe (at time t) divided by Planck time (or, to put it another way, the magnitude of the age of the universe when expressed in Planck time).  Or, as I have used frequently elsewhere, ꬱ (first introduced in Avoiding a Contravention of the Extended Consistency Principles).  It’s a useful term in that context, but not so much when mixed up with the notion of a confused (reduced? raised?) Compton frequency.

---

I did reach out to Haug to discuss the above but have not, yet, heard back from him.

---

* There's a little oversimplification here.  Keen-eyed readers will note that M has not been explained here.  It's not quite the mass of the universe, because in a flat universe, the mass is m_P.ꬱ/2.  To understand what is going on a review of The Conservatory - Notes on the Universe might help.  In brief though, if we think of a standing wave between two nodes (null points), then the minimum full wavelength is twice the minimum distance possible between nodes - because there is a node in the middle of a full wavelength.  The consequence of this, if we have granularity (as in a FUGE Universe), is that when the universe expands by one Planck length, there is one additional node added, allowing for one more half wavelength, or λ(t)=c.t/2.  Each half wavelength corresponds to an extra half a unit of Planck mass/energy, so the M value above (if it were the mass of the universe) would be M(t)=m_P/2.t/t_P.

Note that because, in the FUGE conception, increments are in half wavelengths, Haug’s “factor” would become (noting the caveats above):

No, Eugene Tatum, Hawking Temperature is not Related to CMB

When I first wrote about redshift (in the context of the OE Curve), about six months ago, I took a pretty hard turn (away from) and ended up mostly covering the ideas of Eugene Tatum, who has quite a few papers out with various colleagues, mostly self-published and with no discernible peer review. I have now broken out the redshift discussion into a separate article and am using this article to focus properly on some key equations from Tatum’s “flat space cosmology”.

---

The first thing to note is that Tatum’s flat space cosmology (FSC) is a model of the universe that is:

flat (“cosmic radius R and total mass M follow the Schwarzschild formula … at all times”),

expands such that the “cosmic event horizon” expands at R=ct (“the cosmic event horizon translates at speed of light c with respect to its geometric center”), and

has a Hubble parameter such that H=1/t, where t is the age of the universe (“(the) cosmic Hubble parameter H can be expressed as c/R and Hubble time (universal age) can be expressed as R/c for any stage of cosmic expansion”).

These are all consistent with a FUGE universe, so it was very exciting to see someone else working on a similar idea with a large number of papers published and a raft of supporting equations.

Tatum goes beyond a FUGE universe however when he introduces the notion of “(the) cosmic linear velocity of rotation” which he calls an angular velocity (without initially introducing a 2π term) and goes on to say, after mentioning Hawking’s black hole temperature formula, that “at any radius R the cosmic temperature T is inversely proportional to the geometric mean of cosmic total mass M and Planck mass”.

Note that, while some close reading is required, it clear in context that, by “cosmic temperature”, Tatum means the CMB radiation temperature, which today is determined to be 2.725K.

---

To understand why there are problems with Tatum’s equation(s), we must take a look at Hawking (radiation) temperature.  For any black hole of mass M, there is an associated temperature given by:

For both a FUGE universe and a universe with FSC, the mass of the universe of radius R=ct is given by M=m_P/2*R/ct_P=m_P/2*t/t_P, where m_P is the Planck mass, and t_P is the Planck time.

That value, assuming a universe that is t₀=t_now=13.8 billion years old, is M_now=8.79×10⁵²kg.  The corresponding Hawking temperature, for a black hole with a radius R_S=R_now=ct_now, would be T_{H_now}=1.40x10^-30K, which is substantially less than the CMB radiation temperature today (2.725K).

Tatum does not claim however that the CMB temperature is equal to the Hawking temperature of a black hole with “cosmic radius” of the universe, merely that there is a relationship, which he establishes (in Solving the Hubble Tension by Extracting Current CMB Temperature from the Union2 Supernova Database) as:

First note that I have changed all of his subscripts for clarity, since he used T_CMB,0, k_b, M_H (referring to the radius when H(t)=H₀ rather than Hawking, as it means in T_H) and m_p.  Tatum’s use of subscripts is quite inconsistent, with Planck units sometimes getting _pl or _Pl, current values getting ₀, _H, _r and _R.

Second note that Tatum points out that his equation is “quite similar” to the Hawking radiation temperature formula.  I would put it differently, what he is effectively claiming is that:

Noting that M_now=m_P/2*t_now/t_P:

We calculated above that T_{H_now}=1.40x10^-30K, and t_now/t_P=8.08×10⁶⁰ (if t=13.8 billion years), so:

This is about right, so that is indeed intriguing.  However, if we look at the standard time for when the CMB was formed – the decoupling/recombination event at t_d=380,000 years, when t_d/t_P=2.22×10⁵⁷ and the T_{H_d}=5.07×10^-26K – we get:

So what we have here is a deviation from the Standard Model and what we understand about decoupling/recombination (hence use of the symbol “≠”), specifically that the temperature at that time had to be ~3000K.

In a FUGE universe, and indeed with FSC, the universe does not expand at a rate of H(t)=2/3t after decoupling/recombination (and in fact it doesn’t in the Standard Model either, or at least not for the entire period, but that’s another issue). 

Instead, with a flat universe, H(t)=1/t so the timing of decoupling/recombination is not the same as for the Standard Model.  In a flat universe, t_d=12.5 million years, when t_d/t_P=7.32×10⁵⁷ and the T_{H_d}=1.54×10^-27 K, meaning that:

This is effectively a proof that Tatum’s equation is invalid.  By coincidence, it works for current values (with an error of about 3%), but fails for past and future values.

---

While working through this, I noticed some other errors.  For example, in The Basics of Flat Space Cosmology (where he lays out FSC), Tatum starts the equation with:

He doesn’t derive this equation but it’s not the relationship that I have issues with, but the use of the equivalence symbol.  Here’s the derivation, for a flat universe (both FUGE and FSC), noting that M_R is the mass of the universe when it has a cosmic radius of R=ct, where t is the age of the universe:

So noting that R=ct, we get the equation above.  But it’s not approximately equal to, it’s precisely equal to, so “=” should be used, not “≅”.

Saying that the Hubble parameter is angular velocity just seems to be nonsense (where is the 2π term?), and the notion of a Planck mass angular velocity is nonsense on top of nonsense – as is the later discussion of “galactic revolving speed” (in which, again the obligatory 2π term is forgotten).  The Hubble parameter in any flat universe model is merely the inverse age of the universe, nothing more.  For that reason, in the discussion below, I will either ignore any term in which Tatum uses any form of ω, or I will replace it with 1/t, which it clearly equates to given that he states that ω≅c/R≅H, again with erroneous use of “≅”.

That all, I want to look more closely at the third equation.  Making all the following subscripts consistent as discussed above:

I have put the “≠” in there to highlight that there is an issue, one that follows through from an error made in the second equation in which Tatum writes (again with error highlighted):

In the final term, they divided by two in the wrong spot.  It should have been within the square root, so:

This means the third equation should have been:

This is probably not news to Tatum though, because in Solving the Hubble Tension by Extracting Current CMB Temperature from the Union2 Supernova Database, the full first equation as presented is:

It still doesn’t work for any value other than those that apply right now, but he has fixed at least one problem (albeit without fixing the reference [The Basics of Flat Space Cosmology] used as support for quoting this equation).

Past Values of the Hubble Parameter

I have tried to look up past values of the Hubble parameter a number of times now, without luck.  Even finding an equation for past values of the Hubble parameter is challenging.  Below is an effort to provide such an equation.

The Hubble parameter is defined as:

And it is stated that:

 

Where the deceleration parameter is defined as:

 

If a=t, as in a FUGE universe and presumably the flat cosmology model as well, then we would have the following:

If a=t^½, as per the radiation-dominated era in the Standard Model, we would have:

 

If a=t^⅔, as per the matter-dominated era in the Standard Model, we would have:

In the Standard Model, the current era is dominated by Dark Energy and, for that reason, we could say that a=e^H.t, where the Hubble parameter no longer changes as is equal to H₀, in which case:

It is interesting that we have three eras where the equations work perfectly with nice tidy values for the deceleration parameter in those eras.  It would be madness to think of the eras as punctuated by sudden flips to a new value, even if Standard Model does otherwise have some identified issues (see The Problem(s) with the Standard Model).  For this reason, we could look at generalising.

Say that a=t^η, where η is a constant.  Then we would have:

Looking at the equation of state, we can see that it would follow (“(i)f the (perfect) fluid is the dominant form of matter in a flat (and isotropic) universe”) that η=2/(3(1+w).  For a matter-dominated era, w=0, so η=⅔.  For a radiation-dominated era, w=⅓, so η=½.  For a dark-energy-dominated era, w=-1, so there is no valid value of η.  For a FUGE universe, w=-⅓, so η=1.  So we don’t really need η, we can use the standard formulation with the equation of state value, w, except for when it doesn’t work of course (in a dark-energy-dominated era – where we would have a division by zero error).

Note that we are still left with one discontinuity point.  It is unclear and where the scale factor changed from the form a=t^η to a=(e^H_0.t)/B (where B is notionally a constant such that B=e^H_0.t_0, where t₀ notionally means "now", but the value of "now" could be applied to any time since that transition to obtain a(t₀)=1 unless, for some reason, we are in a privileged era).

---

To work out the value of H(t) in the past then, we just need to know what t is.  I ask this because it makes sense that t is the age of the universe (and in this context it is for a FUGE universe), but this is not stated explicitly in the documents that I have looked at.  The closest to an explicit statement is that we can compare two values of a(t), one now at time t₀ and another at time t.  This implies that we can use now as the reference and the value of t in the equation is now minus how long ago an event at time t happened.  If we take “now” as being the age of the universe, then t will be the age of the universe at that time.

The most likely reason that people working in this area avoid just saying that t is the age of the universe is that they use the value t_H=1/H₀, which is reported as both 13.79 billion years and 14.4 billion years (with the latter being more common).  This is despite there being the Hubble tension, which means that the Hubble time should be presented with much less certainty, to match the lack of overall certainty associated with the Hubble parameter value (which is very close 76km/s/Mpc [Cepheids], somewhere close to 71km/s/Mpc [Standard Sirens] or very close to 67km/s/Mpc [CMB]).  It’s more accurate to say that the Hubble time, as defined as t_H=1/H₀, falls somewhere in the region of 12.8 to 14.6 billion years (and somewhere around 13.8 billion years according to the Standard Sirens value).

---

We can bite the bullet and say that t in H(t) is the age of the universe where the current age of the universe is in the region of t≈14 billion years (13.8 if you like artificial certainty), so H₀≈70km/s/Mpc.

Going further to establish the values that I actually want (for an earlier but recently updated article on redshift), namely the Hubble parameter value for the decoupling/recombination event, we can say that for the Standard Model:

H(380,000 years)=2/3/(380,000 years)=1,720,000km/s/Mpc

And for a FUGE universe (see  FUGE and Redshift):

H(12.5 million years)=(1/12.5 million years)=78,200km/s/Mpc

FUGE and Redshift

I have written before about the OE Curve and redshift, but it was blended together with consideration of someone else’s theory about the universe so it’s not as clear as I would have liked.  So, I’ll have another go at it.

---

There are (at least) two ways to think about redshift.

A photon which is emitted by a source that is moving away at a sufficiently high speed can be observed to be redshifted.  That’s not to say there isn’t redshift for slow (non-relativistic) light sources, it’s just that the redshift in that case is so small as to be unobservable.  This form of redshift is effectively the same as Doppler shift, but requires some extra thought due to relativistic effects (see relativistic Doppler shift).

A photon that is emitted by a source that is stationary (at rest relative to the Hubble flow) or “comoving” relative to the observer, if sufficiently distant from that observer, can also be observed to be redshifted.  Again, the redshift is there, irrespective of the distance under those conditions, but at relatively short distances it’s too small to be observed.

(There is a third source of redshift, which is due to gravity.  It’s actually similar to the redshift due to cosmological expansion in a way, but at a different scale, since both involve deformation of space along the path of the photon.  Redshift due to gravity occurs when the photon is moving out from a gravitational field.)

I want to address redshift due to cosmological expansion.  First think about a photon moving through space in a given direction.  It has a wavelength determined by the speed of light, since a photon is a wavelet oscillating with a frequency determined by its energy (which is related to its colour and associated temperature).  That wave traces a path through space like this:

Say we stretch the original space illustrated above by a factor of two (looking at only the first full wavelength), we now get this:

The speed of light remains constant, so what we have here is a photon with twice the wavelength and half the frequency.  It’s an extreme case of redshifting.

To determine the redshift, z, we take the second wavelength, λ_now, subtract the original wavelength, λ_then, and divide by the first wavelength:

z=(λ_now-λ_then)/λ_then=(λ_now/λ_then)-1

Or,

z+1=λ_now/λ_then

Note that this equation is the same as standard redshift, where now=obsv and then=emit.

In a FUGE universe, the radius of the universe at a given time t will be ct.  The wavelength of an arbitrary photon at that time will be some fraction of that radius, so we can consider a photon of wavelength λ_then=ct_then/B.  After a period of expansion that same photon (now) will have the wavelength λ_now=ct_now/B.  Substituting this into the above and we get:

z+1=t_now/t_then

Alternatively, we can think about scale factor over time.  In a FUGE universe, a(t)=ct/ct₀ where is a reference time (usually now, but it doesn’t have to be in the case).  Note that cosmological redshift is given by

z+1=a_now/a_then

So using the scale factor equation above:

z+1=(ct_now/ct₀)/(ct_then/ct₀)

z+1=t_now/t_then

Alternatively, we can think about the OE curve, for which the equation is x'=(ct₀-x).x/ct₀.  Note that this could be confusing, because in all the OE curve articles in which I clarify that x=ct, I use t to refer to the time elapsed between emission time of the photon (or when it was in a particular location) and the observer.  The t used above (and in the redshift literature more generally) is a reference to the age of the universe (for which I use ꬱ).  Also, in the OE curve equation, rather than being just a reference time, t₀ is specifically the current period of time since the beginning of the universe, or perhaps less confusingly t₀ is the current age of the universe, so t_now=t₀.

I do note, in Mathematics for Taking Another Look at the Universe, that in the OE curve equation it would be more accurate to say that it would be more accurate to use Δt and Δx, so Δx=c.Δt and thus

x'=(ct₀-Δx).Δx/ct₀=(ct₀-cΔt).cΔt/ct₀

I’ll use this notation for as much clarity as is possible under the circumstances, noting that Δt is referring to the delta between now and then, so Δt=t_now-t_then=t₀-t_then, and Δx=ct is the distance a photon in static space would travel in that time.

Consider, hypothetically, that redshift might be due to the difference between the actual separation crossed and the distance that the photon needed to travel to cross that separation, or:

z=Δx/x'

Note that what this is effectively doing is comparing the distance between two comoving locations (emitter and observer) at two times (relative to the observer), time of emission and time of observation.

Substituting in the OE curve equation:

z=Δx/((ct₀-Δx).Δx/ct₀)

z=ct₀/(ct₀-Δx)

Noting that Δx=c.Δt:

z=t₀/(t₀-Δt)

And then noting that Δt=t₀-t_then and t₀=t_now:

z=t_now/t_then

This isn’t precisely the same as above, but for sufficiently high values of z, z+1≈z, so it’s a good approximation.

---

The problem, of course, as identified in the earlier article about redshift, is that the value for CMB redshift calculated this way is in the order of z≈36,000 (assuming t_d=380,000 years).  The accepted value is z≈1100.

However, this value is based on the assumption that the universe expanded such that H(t)=2/3t since decoupling/recombination (at t=t_d) which in turn would mean that z=(t_d/t₀)^⅔.  Note that 36,000^⅔≈1100.

If the FUGE universe model were to be correct, the redshift value associated with the CMB would remain z=1100, because this is required to reach the temperature at decoupling/recombination, but the timing of decoupling/recombination would be different.  In a FUGE universe, H(t)=1/t, and therefore the 2/3 power factor disappears, leaving us with z=t_d/t₀, such that decoupling/recombination would have happened at t_d≈12.5 million years (leaving plenty of time for the development of the oldest stars – including Methuselah – which are calculated to be in the order of 12 to 13.7 billion years old).

---

There’s another aspect of redshift, which I haven’t really mentioned above, which is the shift in colour.  The colour of a photon is related to its wavelength – red photons have a wavelength in the region 625-740 nm.  Blue photons have a wavelength in the region 450-495nm.  You can see, therefore, that as a photon’s wavelength is increased, its colour is changed in the red direction.

If the colour of a photon is pushed even further, it leaves the visible spectrum into infrared and eventually into the microwave spectrum (pushing it further you could even get radio waves).

We can think of the CMB as being a blackbody radiation spectrum associated 2.75K and indeed the correspondence is nigh on perfect with that (source):

The find the peak of this spectrum, we can use Wein’s displacement law, λ_max=b/T, where b(=2.897×10^-3 m.K) is the constant of proportionality and T is the temperature in kelvin.

Given the current temperature and the temperature at decoupling/recombination (t_d=3000K), we can work out the wavelengths:

λ_{max_CMB}(t₀)=2.897×10^-3/2.75=1.05×10^-3m

λ_{max_CMB}(t_d)=2.897×10^-3/3000=966×10^-9m

Note that this latter wavelength actually corresponds with infrared and the first, unsurprisingly, is in the microwave spectrum.

---

There is another way to arrive at a value of redshift in a FUGE universe.  This is via equations in notes from Oxford university (3.c. (Solution)), where it is stated that H(t_d)=H₀.1000√1000 and that (t_d/t₀)^⅔=1/1000.  If so, then it follows that (H(t_d)/H₀)^⅔=1000=(t₀/t_d)^⅔, and thus H(t_d)/H₀=t₀/t_d.  Since t₀=t_now and, in this instance, t_d=t_then, we have:

z≈t_now/t_then=H(t_then)/H(t_now)

Again, this should come as no surprise as, in a FUGE universe, H(t)=1/t.  However, if there were any direct evidence that, at decoupling/recombination, the value of the Hubble parameter was in fact H(t_d)≈ 77,000, see Past Values of the Hubble Parameter, then we’d have another way to work out that z_CMB≈1100.

Note that in the Standard model, H(t_now)=H₀≈70km/s/Mpc (using the centre point of the values per the Hubble tension) and H(t_d)=2/3t_d.  Using the Standard Model value of 380,000 years, that is H(t)=1,720,000km/s/Mpc.

---

In conclusion, the FUGE universe model is consistent with redshift as we know it.  There are a number of ways of looking at it with all results being consistent, although the timing of decoupling/recombination is different due to the different rate of expansion between then and now.