When I first wrote about redshift (in the context of the OE Curve), about six months ago, I took a pretty hard turn (away from) and ended up mostly covering the ideas of Eugene Tatum, who has quite a few papers out with various colleagues, mostly self-published and with no discernible peer review. I have now broken out the redshift discussion into a separate article and am using this article to focus properly on some key equations from Tatum’s “flat space cosmology”.
---
The first thing to note is that Tatum’s flat space cosmology (FSC) is a model of the universe that is:
flat (“cosmic radius R and total
mass M follow the Schwarzschild formula … at all times”),
expands such that the “cosmic event
horizon” expands at R=ct (“the cosmic event horizon translates at speed
of light c with respect to its geometric center”), and
has a Hubble parameter such that H=1/t,
where t is the age of the universe (“(the) cosmic Hubble parameter H
can be expressed as c/R and Hubble time (universal age) can be expressed
as R/c for any stage of cosmic expansion”).
These are all consistent with a FUGE universe, so it was very
exciting to see someone else working on a similar idea with a large number of papers
published and a raft of supporting equations.
Tatum goes beyond a FUGE universe however when he introduces
the notion of “(the) cosmic linear velocity of rotation” which he calls an
angular velocity (without initially introducing a 2π term) and goes on to say, after
mentioning Hawking’s black hole temperature formula, that “at any radius R
the cosmic temperature T is inversely proportional to the geometric mean
of cosmic total mass M and Planck mass”.
Note that, while some close reading is required, it clear in
context that, by “cosmic temperature”, Tatum means the CMB radiation temperature, which
today is determined to be 2.725K.
---
To understand why there are problems with Tatum’s
equation(s), we must take a look at Hawking (radiation) temperature. For any black hole of mass M, there is an associated
temperature given by:
For both a FUGE universe and a universe with FSC, the mass of the universe of radius R=ct is
given by M=mP/2*R/ctP=mP/2*t/tP, where mP
is the Planck mass, and tP
is the Planck time.
That value, assuming a universe that is t0=tnow=13.8
billion years old, is Mnow=8.79×1052kg.
The corresponding Hawking temperature, for a black hole with a radius RS=Rnow=ctnow,
would be TH_now=1.40x10-30K, which is
substantially less than the CMB radiation temperature today (2.725K).
Tatum does not claim however that the CMB temperature is
equal to the Hawking temperature of a black hole with “cosmic radius” of the
universe, merely that there is a relationship, which he establishes (in Solving the Hubble Tension by
Extracting Current CMB Temperature from the Union2 Supernova Database)
as:
First note that I have changed all of his subscripts for
clarity, since he used TCMB,0, kb, MH (referring
to the radius when H(t)=H0 rather than Hawking, as it means in TH)
and mp. Tatum’s use of
subscripts is quite inconsistent, with Planck units sometimes getting pl
or Pl, current values getting 0, H,
r and R.
Second note that Tatum points out that his equation is
“quite similar” to the Hawking radiation temperature formula. I would put it differently, what he is effectively
claiming is that:
Noting that Mnow=mP/2*tnow/tP:
We calculated above that TH_now=1.40x10-30K,
and tnow/tP=8.08×1060 (if t=13.8 billion years), so:
This is about right, so that is indeed intriguing. However, if we look at the standard time for
when the CMB was formed – the decoupling/recombination event at td=380,000 years, when td/tP=2.22×1057 and the TH_d=5.07×10-26K – we get:
So what we have here is a deviation from the Standard Model
and what we understand about decoupling/recombination (hence use of the symbol
“≠”), specifically that the
temperature at that time had to be ~3000K.
In a FUGE universe, and indeed with FSC, the universe does
not expand at a rate of H(t)=2/3t after decoupling/recombination (and in
fact it doesn’t in the Standard Model either, or at least not for the entire
period, but that’s another issue).
Instead, with a flat universe, H(t)=1/t so the timing
of decoupling/recombination is not the same as for the Standard Model. In a flat universe, td=12.5
million years, when td/tP=7.32×1057 and the TH_d=1.54×10-27 K, meaning
that:
This is effectively a proof that Tatum’s equation is
invalid. By coincidence, it works for
current values (with an error of about 3%), but fails for past and future
values.
---
While working through this, I noticed some other errors. For example, in The Basics of Flat Space Cosmology (where he lays out FSC), Tatum starts the equation with:
He doesn’t derive this equation but it’s not the relationship that I have issues with, but the use of the equivalence symbol. Here’s the derivation, for a flat universe (both FUGE and FSC), noting that MR is the mass of the universe when it has a cosmic radius of R=ct, where t is the age of the universe:
So noting that R=ct, we get the equation above. But it’s not approximately
equal to, it’s precisely equal to, so “=” should be used, not “≅”.
Saying that the Hubble parameter is angular velocity just
seems to be nonsense (where is the 2π term?), and the notion of a Planck mass angular velocity is
nonsense on top of nonsense – as is the later discussion of “galactic revolving
speed” (in which, again the obligatory 2π term is forgotten). The
Hubble parameter in any flat universe model is merely the inverse age of the
universe, nothing more. For that reason,
in the discussion below, I will either ignore any term in which Tatum uses any
form of ω, or I will
replace it with 1/t, which it clearly equates to given that he states that ω≅c/R≅H, again with erroneous
use of “≅”.
That all, I want to
look more closely at the third equation.
Making all the following subscripts consistent as discussed above:
I have put the “≠” in there to highlight that there is an
issue, one that follows through from an error made in the second
equation in which Tatum writes (again with error highlighted):
In the final term, they divided by two in
the wrong spot. It should have been within
the square root, so:
This means the third equation should have
been:
This is probably not news to Tatum
though, because in Solving
the Hubble Tension by Extracting Current CMB Temperature from the Union2
Supernova Database, the full first equation as presented is:
It still doesn’t work for any value other
than those that apply right now, but he has fixed at least one problem (albeit without
fixing the reference [The Basics of Flat Space Cosmology]
used as support for quoting this equation).
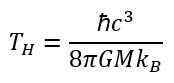











No comments:
Post a Comment
Feel free to comment, but play nicely!
Sadly, the unremitting attention of a spambot means you may have to verify your humanity.