I have tried to look up past values of the Hubble parameter a number of times now, without luck. Even finding an equation for past values of the Hubble parameter is challenging. Below is an effort to provide such an equation.
The Hubble parameter is defined as:
And it is stated that:
Where the deceleration parameter is defined as:
If a=t, as in a FUGE universe and
presumably the flat cosmology model as well, then we would have the following:
If a=t½, as per the
radiation-dominated era in the Standard Model, we would have:
If a=t⅔, as per the matter-dominated era in the Standard Model, we would have:
In the Standard Model, the current era is dominated by Dark Energy and, for that reason, we could say that a=eH.t, where the Hubble parameter no longer changes as is equal to H0, in which case:
It is interesting that we have three eras
where the equations work perfectly with nice tidy values for the deceleration
parameter in those eras. It would be
madness to think of the eras as punctuated by sudden flips to a new value, even
if Standard Model does otherwise have some identified issues (see The Problem(s) with the Standard Model). For this reason, we could look at generalising.
Say that a=tη, where η is a constant. Then we would have:
Looking at the equation
of state, we can see
that it would follow (“(i)f the (perfect) fluid is the dominant form of matter
in a flat (and isotropic) universe”) that η=2/(3(1+w). For
a matter-dominated era, w=0, so η=⅔. For
a radiation-dominated era, w=⅓, so η=½. For a dark-energy-dominated era, w=-1,
so there is no valid value of η. For a FUGE universe, w=-⅓, so η=1. So we don’t really need η,
we can use the standard formulation with the equation of state value, w,
except for when it doesn’t work of course (in a dark-energy-dominated era – where we would have a division by zero error).
Note that we are still left with one discontinuity point. It is unclear and where the scale factor changed from the form a=tη to a=(eH_0.t)/B (where B is notionally a constant such that B=eH_0.t_0, where t0 notionally means "now", but the value of "now" could be applied to any time since that transition to obtain a(t0)=1 unless, for some reason, we are in a privileged era).
---
To work out the
value of H(t) in the past then, we just need to know what t is. I ask this because it makes sense that t
is the age of the universe (and in this context it is for a FUGE universe), but
this is not stated explicitly in the documents that I have looked at. The closest to an explicit statement is that we
can compare two values of a(t), one now at time t0 and
another at time t. This implies
that we can use now as the reference and the value of t in the equation
is now minus how long ago an event at time t happened. If we take “now” as being the age of the
universe, then t will be the age of the universe at that time.
The most likely
reason that people working in this area avoid just saying that t is the
age of the universe is that they use the value tH=1/H0,
which is reported as both 13.79
billion years and 14.4
billion years (with the
latter being more common). This is
despite there being the Hubble
tension, which means
that the Hubble time should be presented with much less certainty, to match the
lack of overall certainty associated with the Hubble parameter value (which is very
close 76km/s/Mpc [Cepheids], somewhere close to 71km/s/Mpc [Standard Sirens] or
very close to 67km/s/Mpc [CMB]). It’s
more accurate to say that the Hubble time, as defined as tH=1/H0,
falls somewhere in the region of 12.8 to 14.6 billion years (and somewhere
around 13.8 billion years according to the Standard Sirens value).
---
We can bite the
bullet and say that t in H(t) is the age of the universe where
the current age of the universe is in the region of t≈14 billion years
(13.8 if you like artificial certainty), so H0≈70km/s/Mpc.
Going further to
establish the values that I actually want (for an earlier but recently updated article
on redshift), namely the Hubble parameter value for the
decoupling/recombination event, we can say that for the Standard Model:
H(380,000
years)=2/3/(380,000 years)=1,720,000km/s/Mpc
And for a FUGE
universe (see FUGE
and Redshift):
H(12.5 million
years)=(1/12.5 million years)=78,200km/s/Mpc






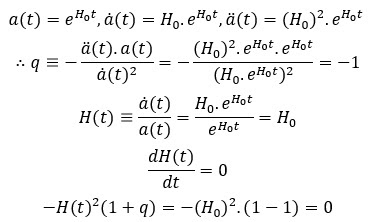

No comments:
Post a Comment
Feel free to comment, but play nicely!
Sadly, the unremitting attention of a spambot means you may have to verify your humanity.