A Minor Departure from MOND

In Towards a physical interpretation of MOND's a0, I arrive at the conclusion that, maybe, a₀=cH/2 has a better basis than the more commonly quoted a₀≈cH/2π.  In the process of doing so, I call upon the value G.

It should be noted that Milgrom makes this statement:

A₀ is the “scale invariant” gravitational constant that replaces G in the deep-MOND limit. … a₀≡A₀/G (…) delineat(es) the boundary between the G-controlled standard dynamics and the A₀-controlled deep-MOND limit.

He also talks in terms of “departures”:

relativity departing from Newtonian dynamics for speeds near the speed of light

and

quantum theory departing from classical physics for values of the action of order or smaller than ℏ

and

a sweeping departure from standard (ed. ie Newtonian) dynamics at low accelerations

It seems to me that, at least in my derivation, there’s an issue with using G that way, I am using a situation where there is a borderline acceleration namely gravity that would manifest at the surface of a black hole with the [critical] density of our universe such that g_U=a₀, which is dependant on a specific value of G.  Note also that G is, in a sense, already scale invariant.  It has a value of unity, unless one departs from natural units (such as Planck units) and instead uses arbitrary units (such as SI units).

Note that my problem is not with a₀, but more with the idea of this variable gravitational constant.

As Sabine Hossenfelder notes (before noting that MOND “doesn’t work” [her quotation marks]), MOND does a nice job of explaining the why outermost stars of a spiral galaxy orbit faster than the mass of the galaxy alone in a Newtonian regime would permit.  But I don’t think we need to fiddle with G to get there.

---

Getting back to “departures”, it’s unclear precisely how Milgrom means the term, but listening to Pavel Kroupa, a proponent of MOND and the author of The dark matter crisis: falsification of the current standard model of cosmology, there are those working on MOND who see it as more benign.  Newtonian mechanics are perfectly good for working out how the solar system works.  Until you notice small perturbations in the orbit of Mercury and General Relativity is needed.  General Relativity is just a better approximation of how things work, it’s not that Newtonian mechanics are wrong.  You can (and, if you want to get things done, should) ignore Einstein if you are considering slow moving things in regions of constant, relatively low gravity and just use Newton.  But you could use Einstein.

I suspect that the same thing is going to happen with MOND.  Whatever equation eventually falls out of the work (the “deeper physics” as Kroupa puts it), it should be the case that that equation can be used in both “regimes”, Newtonian and (deep-)MOND.

---

According to Angus et al. there is an interpolating function μ(x), such that for x<<1, μ(x)=x, and for x>>1, μ(x)=1 where μ(g/a₀)g=g_N (and thus μ(g/a₀) =g_N/g).  Note that g_N is Newtonian gravity due just to baryons while g is the observed, “overall” gravity.

The standard interpolating function used to fit to rotation curves is μ(x)=x/√(1+x²).  This can also be expressed as μ(x)=1/√(1/x²+1).  And putting it to use where x=g/a₀, we get μ(g/a₀)=1/√( /a₀²/g²+1)=g_N/g.

The comment made in the linked paper is that “there is a considerable body of evidence that the galactic mass profiles of baryonic and dark matter are not uncorrelated”.  The authors tagged this as “curious”, but what I find curious is that they say “not uncorrelated” rather than saying “correlated”.  The reason, if I understand it correctly, is that the correlation is back to front.  With the standard interpolating function as given (and even more so in the replacement version that the authors suggest), one can only calculate the effect of baryonic matter (the actual matter that we know exists and isn’t merely theoretical) if you know the “overall” mass profile (including an overwhelming quantity of dark matter).  You can’t, in any simple way, start off with so much baryonic matter and work out that we have this much dark matter.

I don’t like this.

---

Let us instead say that gravitation due to an ordinary baryonic mass M at any radius r is given by:

g = GM/r²+√(GMa₀)/r = g_N+√(GMa₀/r²) = g_N+√(g_Na₀)

The consequence of this is that both terms will diminish as the radius r increases, with the former dominating until its value approaches a₀.  As r increases beyond that point, the latter term will begin to dominate.

Putting this into similar terms as above (parameterising the correlation and specifying the implied interpolating function):

μ(a₀/g_N)g_N=g where μ(x)=1+√x, so that where a₀<<g_N, g=g_N and where a₀>>g_N, g=√(g_Na₀).

Personally, I don’t think this makes things much clearer, although I do realise that the relationship is not immediately obvious from the first equation above.

---

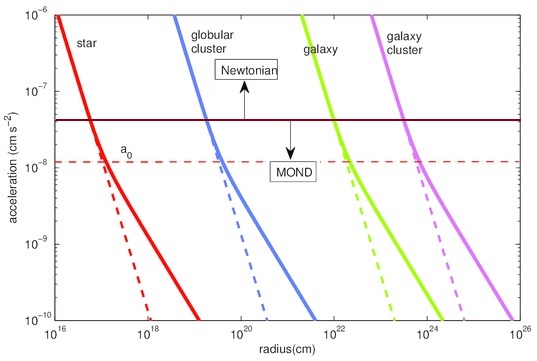
When this correlation is charted for four types of mass, a star, a globular cluster, a galaxy and a galaxy cluster (using the same masses as used by Milgrom, see below), we get this (where a₀=cH/2):

Compare this with Milgrom’s chart (where a₀=1.2×10^-10m/s²=1.2×10^-8cm/s², a star is one solar mass, the globular cluster is 100,000 solar masses, a galaxy is 30 billion solar masses [at the very low end of the mass of the Milky Way in terms of known baryonic matter only] and galaxy cluster is 30 trillion solar masses):

I tried to regenerate this my own way, to use Milgrom’s version of a₀, while using the more common m rather than cm, but I get this:

Note that the departure from the Newtonian regime begins much earlier and is greater in magnitude in the transition range (which is basically what is shown).

I can overlay the two charts using different values for a₀:

The effect due to using a different value of a₀ appears to be marginal.  However, it should not be forgotten that the axes here are using a logarithmic scale.  It should also not be forgotten what MOND (and dark matter) is being postulated to explain.

Consider a spiral galaxy, like our Milky Way:

What astronomers observed is that stars in the outer arms are going faster than could otherwise be expected given the mass of the galaxy.  So, either there is extra mass in the galaxy that we can’t detect (dark matter) or there is some gravitational effect that we don’t fully understand (MOND).

Strictly speaking, you don’t have one mass orbiting another mass, they both orbit the centre of their combined masses, but when one is vastly greater than the other, we consider the larger to be the one being orbited by the other.  In that case, we can consider a smaller mass to have an orbital velocity around the larger mass, M, such that the acceleration towards the centre is balanced by the centripetal force outwards, normally:

F=ma=GMm/r²=mv²/r

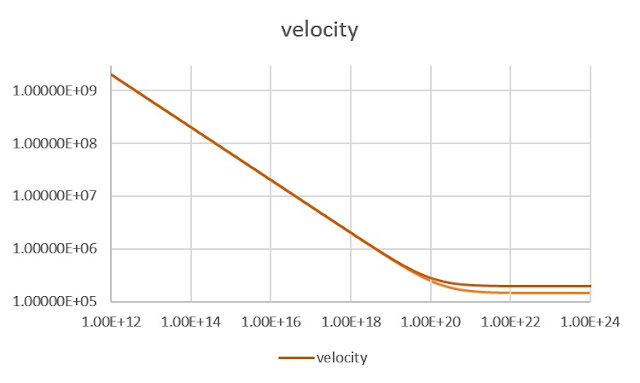
Such that v=√(a.r)=√(GM/r).  What we can do now is calculate the effect of MOND (where a₀=ch/2) on the orbital velocities.  Since the curves are similar for stars, galaxies, etc, we can just use a galaxy. 

Note that once we get out to about 10,000 light years from the galactic core, the orbital velocity is basically constant from then on out.  The Milky Way is 100,000 light years across. 

Once we have calculated the orbital velocity, we can consider the quantity of mass required in a Newtonian regime to have that orbital velocity at the relevant radius, using M_eff=rv²/G, as a proportion of the actual mass of the galaxy (notionally 30 billion solar masses, or 6×10⁴⁰kg):

Now this doesn’t look like much, but again, remember that this is a logarithmic scale.  The darker mass curve is mine, representing MOND with an a₀=cH/2.  The delta is, once they level out, consistently such that the effective mass is in the order of 77.25% higher than with a₀=cH/2π.

Note that Milgrom states “For galaxy clusters, MOND reduces greatly the observed mass discrepancy: from a factor of ∼10, required by standard dynamics, to a factor of about 2.”  Using my alternate version of a₀, this residual discrepancy seems to disappear.

---

Applying this to our solar system, which is orbiting the galactic core at about 250 km/s, or v=230,000m/s, at a radius of about 26,000ly, or about r=2.5×10²⁰m, and assuming H=71 (equating to the universe being 13.77 billion years old) … this would imply that, if a₀=cH/2, the mass of the galaxy is about 30 billion solar masses, or M=6.0×10⁴⁰kg.  To get the same figure orbital velocity at the same distance from the galactic core using the assumption of dark matter, the mass would be about 100 billion solar masses, or M=2.0×10⁴¹kg.  If a₀=cH/2π then, it’d be about 60 billion solar masses, or 1.2×10⁴¹kg.

It appears that these are at the very low end of the range for the mass of the Milky Way, particularly the 30 billion solar masses figure, given that there are some recent estimates that it might be in the order of a trillion solar masses (including dark matter).  However, I have checked and rechecked the figures and that’s what pops out.  Also, this is just the mass within the orbit of our solar system.  We are 26,000 light years from the core, but the Milky Way galaxy is about 100,000 light years across, so some fraction of the mass does not contribute to our orbit around the galactic core, whatever is in the 24,000 light year ring about the sphere defined by our orbit.  This is probably less than a third of the entire mass though (remembering that there’s a super massive black hole at the centre):

It also seems to be what Milgrom arrived at, since he had his galactic mass as 30 billion solar masses and it’s not difficult to assume that he did so, because that’s precisely what is required to have our solar system orbiting the galactic core at 230,000m/s – however, this would be if he was using a₀=cH/2 rather than a₀=cH/2π.  Use of the latter would imply, as indicated above, a galactic mass of closer to 60 billion solar masses and it would be odd of Milgrom to have not used that, especially since he indicates an “observed mass discrepancy” at a factor of 2.

---

There are two other calculations worth looking at, that for the Earth’s orbit around our star, and the value of gravity at the Earth’s surface. 

The Earth has an elliptical orbit at an average radius of 1.496×10¹¹m from the centre of the Sun, which (unsurprisingly) has a mass of one solar mass, or about 2×10³⁰kg.  Using all three methods (pure Newtonian, my MOND and Milgrom’s MOND), the results were within 0.015% of 29,789m/s (when using 1.9891×10³⁰kg as the solar mass).  The accepted average orbital velocity is 29,783m/s.

It should come as no surprise that the value of gravity at the Earth’s surface is also largely unaffected by introducing MOND calculations.  The Earth’s mass is 5.97×10²⁴kg and sea level is at 6.37×10⁶m on average.  In all three methods, the result is 9.82m/s², with the MOND related contribution being a negligible 0.00059% or 0.00033% for a₀=cH/2 and a₀=cH/2π respectively.

---

TLDR:

A potentially better variation of MOND is one in which g=GM/r²+√(GMa₀)/r where a₀=cH/2.  The rotation curves work, the mass discrepancy raised by Milgrom disappears and there is a physical understanding behind the value of a₀.

Towards a physical interpretation of MOND's a0

In MOND, FUGE and Dark Matter Light, there’s a little play on words, based on a comment in Milgrom’s Scholarpedia article The MOND paradigm of modified dynamics:

 

For galaxy clusters, MOND reduces greatly the observed mass discrepancy: from a factor of ∼10, required by standard dynamics, to a factor of about 2. But, this systematically remnant discrepancy is yet to be accounted for.

 

In my post, I highlight that I consider “dark matter” to be more of a phenomenon related to the mass discrepancy, a placeholder if you like until such time as the mass discrepancy is explained.  One solution is an actual form of matter (cold dark matter) and another solution is the a₀ of MOND.  Milgrom seemed to be pointing to the possibility of a midway point, with a little cold dark matter (or missing baryons).

 

---

 

I also, perhaps unadvisedly, said that Milgrom used a form of numeromancy to arrive at his value of a₀, the acceleration constant that is central (mathematically at least) to MOND.  I fiddled around – merely using the units (which could also be called a form of numeromancy) – and found that if a₀=c.H₀/2π, then we get a value of a₀ very close to what Milgrom calculated (~1.2×10^-10m/s²).

 

Now, according to Wikipedia, with no reference provided:

By fitting his law to rotation curve data, Milgrom found a₀ ≈ 1.2×10^-10 m/s² to be optimal.

 

According to Milgrom himself:

a₀ can be determined from several of the MOND laws in which it appears, as well as from more detailed analyses, such as of full rotation curves of galaxies. All of these give consistently a₀≈(1.2±0.2)×10⁻⁸cm s⁻².

 

And later:

Significantly perhaps, it’s measured value coincides with acceleration parameters of cosmological relevance, namely, a¯₀≡2πa₀≈cH₀≈c²(Λ/3)^1/2 (H₀ is the Hubble constant, and Λ the cosmological constant). This adds to several other mysterious coincidences that characterize the mass-discrepancy conundrum, and may provide an important clue to the origin of MOND.

 

So, it wasn’t quite numeromancy.  What I was really objecting to, in my own muddled way, was that there didn’t seem to be a physical meaning to a₀.  Sure, there’s an approximate numerical equivalency between a₀ and c.H₀/2π, but what does that mean?

 

---

 

First off, there’s a problem tying anything to H₀ because of the Hubble tension which has the value of H₀ being 67.4±1.4 km/s/Mpc (CMB data), 67.36±0.54 km/s/Mpc or 67.66±0.42 km/s/Mpc (Planck 2018 data [the latter with BOA data added]), 73.04±1.4 km/s/Mpc (SH0ES data) and 78.3±3.4 km/s/Mpc (the most extreme of the quasar lensing measurements).  If we plug in these values, we would be saying that the value would lie in the range a₀≈1.04m/s² to a₀≈1.21m/s² (if calculated as above).  Milgrom’s value is right at the upper limit.

 

---

 

In the FUGE model, the universe has been expanding by one unit of Planck length every unit of Planck time, and the mass-energy in it has been increasing by half a Planck mass per unit of Planck time.  This results in the density remaining critical throughout.

 

Critical density is given by the equation ρ_c = 3.H²/8πG.  This is the density of a (Schwarzschild) black hole with a radius of r=c/H (explained here).

 

That means that, in the FUGE model, if the universe has an age of approximately æ.t_P=8×10⁶⁰ units of Planck time=13.77 billion years (explained here), then it has H₀=1/(æ.t_P)=1/(13.77 billion years)=71km/s/Mpc (this is just saying that the Hubble value is the inverse of the age of the universe, which is related to how the universe expands), a radius of approximately æ.l_P=8×10⁶⁰ units of Planck length=13.77 billion light year and a mass of approximately (æ.m_P)/2=4×10⁶⁰ units of Planck mass=8.77×10⁵²kg (also explained here).

 

This gives us enough information to ask an odd question.  What is the gravity of the universe at its surface?  There are, of course, obvious objections to this question, which might be why it has not been asked before.  But let me work through it for the purposes of the exercise.

 

Gravity of the Earth is given by the radius of the Earth (more specifically the distance from the centre of the Earth’s mass at which we are considering, we can use sea level, 6,378km), the mass of the Earth in this equation (5.972×10²⁴kg) and the Gravitational Constant G (6.674×10^-11N.m²/kg²):

 g_E=Gm_E/r²=9.8m/s²

 

Using the same method, we could say that the “gravity of the universe” is:

g_U=Gm_E/r²=G.(æ.m_P)/2/(æ.l_P)²

 

We know that m_P=√(ħc/G), l_P=√(ħG/c³) and t_P=√(ħG/c⁵) and thus also that c=l_P/t_P.  So:

g_U=G.(æ.√(ħc/G))/2/æ²/(ħG/c³)=√(ħc/G)/(2.æ.(ħ/c³))

 

Multiplying through by t_P/t_P:

g_U=√(ħc/G).√(ħG/c⁵)/(2.æ.(ħ/c³).√(ħG/c⁵)

 =(ħ/c²)/(2.(æ.t_P).(ħ/c³)=c/(2.(æ.t_P))

 

And because, as mentioned above, H₀=1/(æ.t_P):

g_U=c.H₀/2

 

Now this value is not what Milgrom and others arrived at but my question has to be, is there enough wriggle room in the mapping of the value of a₀ to rotation curve data to allow the π to be dropped?  There may be.  At his Scholarpedia entry, Milgrom has this chart:

Note that the selection of the a₀ value appears arbitrary and signifies the point "below which we are in the MOND regime".  If we consider instead the point above which we are are unequivocally in the Newtonian regime, a different line could be drawn:

 

This could easily equate to a₀=c.H₀/2.

---

 

A TLDR for the above is this:

Consider the critical density of the universe, ρ_c = 3.H²/8πG, this is the same as the density of a (Schwarzschild) black hole with radius r=c/H.  Such a black hole has a mass of M=c³/2GH.  And the gravity at the radius of such a black hole is g=cH/2.  In the FUGE model, there is no inflation and on dark energy, so the radius of the universe would be c/H and a₀=cH/2 could therefore be the “implied gravity” on the “surface” of the universe.

Thinking Problems - Conspiracy Theorists

This is the beginning of, hopefully, a short series of articles on odd thinking.  In line with what I think will emerge as the general theme, the first thing I need to do is define what a “conspiracy theorist” is.

 

For me, it is a matter of perspective, the vantage point from which the conspiracy theorist views a problem, or what they perceive of as a problem.  It isn’t merely that the person believes that there are conspiracies in this world.

 

There have been conspiracies.  Real conspiracies.  The attacks on the Twin Towers, the Pentagon and whatever the other hijacked plane had as its target (that is the hijackers conspired, together with their masters) involved a conspiracy.  There was a conspiracy involved in the coverup of the Watergate burglaries.  There was a conspiracy by Tom Cruise and some other less famous people in the Operation Valkyrie attempt to assassinate Hitler.  There was a conspiracy involved in hiding the effect of tobacco on health.  Volkswagen people conspired falsify emissions data.

 

While these were all real, they were, in a sense, minor conspiracies.  That is to say that they involve only a relatively small number of conspirators and those conspirators only intended to directly impact a relatively small number of people.  For example, the attack on the Twin Towers certainly involved the intentional murder of everyone on the planes, and everyone in the direct impact zone, but they were unlikely to have been confident that they’d bring down both buildings entirely with so many people inside and there was absolutely no intention to conduct the attack in such a way as to make it secret from the whole world.  They didn’t, for example, board the planes with latex masks and voice modifiers, all pretending to be Tom Cruise.

 

There are some massive conspiracies that are real.  Like the Santa conspiracy, perpetrated by almost all western parents (although they might use different code names to maintain the pretence, like Tomten in Sweden, or Sintaklaas in the Netherlands).  Or the concerted effort to make people believe that “Turkish delight” is not disgusting.

 

Knowing that these sorts of conspiracies are real does not make one a “conspiracy theorist”.

 

To be conspiracy theorist, in my definition, requires a pathological mode of theorising that implies one or (usually) more grand conspiracies.  A grand conspiracy involves either a massive number of conspirators or a massive number of victims of the conspiracy (usually everyone bar a few very special people in the know) – or both.  A conspiracy theorist may also have a couple of more mundane conspiracy theories in his arsenal.

 

Note that the implication of a grand conspiracy does not need to be explicit.  To take a ridiculous example, some people think that the Berenstain Bears used to be called the “Berenstein Bears”, but something happened to change the name.  Believing this does not seem at first blush to involve a conspiracy.  However, if you think a little further, the explanations required for the Berenstain Bears to have been called the Berenstein Bears in the past all involve a conspiracy.

 

Perhaps there was a concerted effort to replace all copies of the books and other merchandise with the “new” spelling – which would require massive numbers of people who know the truth and are concealing it from the rest of us (for no apparent reason).

 

Perhaps there is an alternate reality in which they do have a different name and memories from that reality has bled into ours.  This involves other instances, like that for this the phenomenon is named.  Some people remember (incorrectly) that Nelson Mandela died in jail in the 1980’s before he was released to later become the President of South Africa.  Other examples include Froot Loops (which were once called Fruit Loops but only a very long time ago), the Monopoly Man’s monocle (he doesn’t have one), Mona Lisa’s missing smile and any one of a huge number of more personal misrememberings.

 

My personal one is that I used to live three houses from someone who worked at a local car dealership, and I did the afternoon paper-round that covered that car dealership.  I moved away to go to university and during those years, the dealership changed its name.  When I came home to visit a few years later, I mentioned the dealership by its old name and was met with blank stares.  My family and friends all believed that the new name had been its name forever.  (However, a state document that I dug up from the internet shows that the old name that I remember was there from as early as 1964 and they were deregistered 20 years after I finished university.)

 

Clearly, the simplest explanation here is that people have imperfect memories (and change blindness).  The conspiracy theorist explanation is that there are alternative realities that impinge on our – and scientists who are aware of this fact have been hiding it from everyone (for no apparent reason).

 

---

 

A conspiracy theorist does not need be a person who generates a grand conspiracy.  They don’t even need to modify or update a grand conspiracy.  A conspiracy theorist can do those things, of course, alone or in company with like-minded people, but not everyone is so creative.

 

The absolute minimum required to be a conspiracy theorist is a tendency towards grand conspiracy theories – either implicitly or explicitly.

 

This last caveat is important.  As mentioned above, conspiracy theorists, and those on the very edge of becoming a conspiracy theorist – the conspiracy curious – will posit explanations for events that they don’t comprehend in such a way as to imply a grand conspiracy.  They might explain it away by pointing to social forces, but they are still subscribing to an implicit grand conspiracy.  Examples of this often involve science and lone “whistle-blowers”, such as with climate change hoax believers and alien visitation.

 

To believe that climate change is a hoax, someone needs to believe that all the scientists working in the area are making up and/or concealing data and that they have either fooled or co-opted politicians along with the media.  The conspiracy theorist can then rely on a small group of “whistle-blowers” or “heterodoxes” for access to “true” information.  If the heterodox is from a relevant, or sufficiently adjacent, field then all the better.

 

If pushed, the conspiracy theorist will claim that it’s not a conspiracy on the part of any one person or group, merely that scientists and politicians are captured by “a prevailing narrative” and there are social pressures to conform to that narrative (along with some form of social contagion that spreads the narrative).  However, this is implying that all the scientists involved (bar the celebrated heterodoxes) will ignore evidence and/or fabricate evidence to support the sanctioned narratives, and put out papers for peer review with all those who read the papers getting perfectly into line to ignore real evidence and/or accept fabricated evidence so long as it supports a mutually agreed narrative that has been arrived individually en masse.  The effect of this social pressure, it is argued, is to conceal the truth from everyone (including those who are deluding themselves) making this an implicit grand conspiracy.

 

A key element to being a conspiracy theorist, maybe even a defining element, is some level of apophenia – or what could be called “hyperactive pattern recognition”.  This the ability and/or willingness to see patterns even when there aren’t any, or to effectively create patterns by linking together disparate elements and/or enhancing the importance of trivial elements.

 

To some extent, our brains just simply do this.  We don’t have perfect access to all of existence, so we fill in the gaps, and much of the time this works sufficiently well to keep us alive.  Note that staying alive is key to what our brains are doing, so this will introduce a bias into our thinking.  We don’t need to make perfect decisions, we need to avoid making wrong decisions that will kill us.  It’s better to be scared by 90% of strange noises, when it’s nothing, rather than miss the critical 1% when it’s a lion or your neighbour stealing your ass.

 

However, it’s a balance.  If we are constantly on edge, and frequently wasting resources on protecting ourselves from a breeze, then we will have a lower likelihood of passing on our genes.  It’s likely that there is spectrum across which people are sufficiently aware of threats without crippling themselves and at the tail ends we have people who are quite unaware (the sort of people who fall for obvious scams) and people who border on paranoia (including conspiracy theorists).

 

A useful way to address the claims of someone who you might suspect of being a conspiracy theorist is to ask yourself: “If this a rational sounding story and what else would have to be true for the claims to be true?”  If the claims involve or imply that some group is maliciously concealing a truth from the whole world, especially if that group contains a vast number of people, then there’s a fair chance that you are dealing with a conspiracy theorist, even if they have no interest in overt conspiracy theories about who killed JFK or what 5G is “really” all about.

 

Of course, there are times when there is a conspiracy that doesn’t amount to a conspiracy theory.  For example, there might be an actual conspiracy on the part of a wedding party to conceal the fact that the bride slept with the best man but that’s not going to amount to a conspiracy theory.  However, if there were a claim that there was conspiracy to conceal that the bride is actually a reptiloid alien in a human suit (and thus to conceal the knowledge that aliens exist [presumably knowledge that is suppressed by people at the very highest levels], that these aliens are visiting Earth [ditto] and that they are interested in committed, long-term interspecies relationships with humans) … well, that’s probably a claim made by a conspiracy theorist, or one of the drunker uncles.

 

---

 

Earlier, I did say that being a conspiracy theorist is a matter of perspective.

 

Imagine that we are looking at this image, which can be thought of as representing facts:

 

What can we make of this?

 

I can tell you that we should make nothing of it.  It’s taken from a set of 50 pairs of random numbers in Excel (using RAND()), which are assigned as x and y values between 0 and 1, and then randomly assigned as Red, Green, Blue or Purple (25% likelihood each).  These were then graphed, and I tidied it up by removing the dots that were on the edge for aesthetic appeal.

 

But if we didn’t know that, then we could ask what the dots mean.  The proper answer in that case is “We just don’t know.”  If pushed for a hypothesis, we might say that they look like randomly placed dots.

 

However, if we were conspiracy theorists, we might want to know the answer to “why?”  Why are there fewer Red than Blue?  Why are three dots clustered very close together?  Why are there three pairs of dots close together that appear to make the same sort of line about 30 degrees from vertical?  Why is there an apparently line made up of two Red, three Blue and one Purple?  Why is there a rocking horse in the top right corner?  And as conspiracy theorists, we might not accept the answer that there is no reason because conspiracy theorists also tend to have a bias towards assigning agency to events.  There are few coincidences for a conspiracy theorist and “things happen for a reason”.  There’s an interesting question with respect to the crossover between conspiracy theorists and magical thinkers, a question which has been studied formally.

 

It’s entirely possible that some people will see patterns in the image that I simply can’t see – because I can easily accept that there’s no underlying meaning to it and I stop looking.  A conspiracy theorist might keep looking until they find something, irrespective of whether it’s there or not.

 

---

 

So, in conclusion, a “conspiracy theorist” is a person who has a tendency towards believing in conspiracy theories, who holds positions that imply conspiracy theories, who has a relatively high level of hyperactive pattern recognition and/or who is overly enthusiastic in the assignment of agency to events.

Heterodoxy

---

This is a follow-on, in a sense, to the JP sequence.  “JP” is a friend of mine who has some issues with the climate change science and – perhaps more so – the reporting of it.  It’s not just the reporting though, since he has repeatedly expressed his admiration of “heterodoxy” – which he seems to define as having the intellectual bravery to position oneself outside the straitjacket of conventional, “consensus” thinking.

 

Now, I am well aware that many people are heterodox when it comes to one issue or another.  For example, the standard view of cosmological evolution includes a period of inflation.  I have a model which does not include that (see posts about the FUGE model).  Some very famous scientists have been heterodox on one issue or another, and were subsequently proven right.

 

Look at that last sentence and consider what, for a scientist and their subsequent fame, was the major contributing factor.  It was not being heterodox per se, it was being proven right.  That’s rare enough to make the scientist famous.

 

The problem with heterodoxy is that it is almost always the wrong approach, particularly in a scientific context – despite it being very much the right approach in the rare situation when everyone else is wrong.  I may well be wrong about the FUGE model, quite likely entirely, but certainly in some key detail.

 

I’ve written before about my world view, and how I prefer that things that I hold true to be true.  I’m not necessarily bothered with whether the things that I hold true are also held to be true by other people.  I am, however, aware that if many people hold a thing to be true, for a suite of good reasons, then it’s more likely that they are true.  The more things that a person holds to be true that I also hold to be true, so long as they don’t also hold a number of incompatible things to be true, then the more likely it is that I might be able to rely on their judgement on something.  And if everyone does something like this, we can all – as a group – develop a “consensus”.

 

I don’t want to suggest that a having consensus means total agreement on all things.  It’s entirely possible to agree on issues in one area and disagree violently in others (for example, we might both agree that rum and raisin dark chocolate is delicious, but you might be insane enough to think that Turkish vomit [often mislabelled known as “Turkish delight”] is not totally disgusting).

 

To be fair to JP, he was once involved (on the periphery) with a cult-like church denomination with a leader who held great sway over the youthful congregation.  In that environment, everyone was encouraged to think alike and also to overlook the inconsistencies involved (it was a Christian thing, so there were plenty of them).  Anyone daring to differ, a heterodox, was subjected to some pretty major pressure to conform – with a threat of being cast out of the friendship group if they didn’t.  (Even having a conversion-resistant atheist like me as a friend was looked down on.)

 

Being a heterodox in that situation was (to my eyes) a good thing.  Challenge what you are being asked to believe, ask for proof, critically examine any evidence provided, acknowledge the fallacies.

 

I think, however, that heterodoxy – for its own sake – can be taken too far.

 

As I explained to someone recently, there are (at least) six levels of “facts” that we can be presented with:

• Actual facts
• Scientific research into facts
• Interpretation of scientific research into facts
• Journalistic reporting of interpretation of scientific research into facts
• Headlines
• Half-remembered expositions on what might be any of the above (or combinations thereof).

 

We can’t usually access actual facts (outside of mathematics), so I am always recommending that we go back to the original scientific research into facts.  However, it’s entirely possible that research is done poorly, or in a biased manner to reach a predetermined result, and that should be kept in mind during an assessment of any research.  But the best research is not a single entity, the best research is a conglomeration or synthesis of multiple lines of research around actual facts, such that the actual facts can be triangulated.

 

I see it a bit like this in normal circumstances:

 

The circles indicate research results which don’t necessarily precisely match the underlying fact, but (generally, if conducted competently and honestly) cluster around the fact.  A heterodox, by rejecting the consensus, may well end up a long way from the fact – especially if guided by vested interests (like someone who wants you to believe in their version of a sky-fairy, or to not worry about potential human effects on the climate).

 

I certainly do agree that we should be wary of ideological conformity, where we might be tempted to look for other facts if the facts that we are faced with won’t play the game.  However, it always seems relatively easy to identify when ideology is the driving factor.  If someone is trying to argue you into accepting their viewpoint but won’t properly explain their position and is resistant to providing any evidence, willing to jump into an “apologetics” or fallacy-based mode of defending their position, then – in my humble opinion – they are likely driven by ideology, rather than facts.