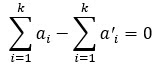So, I was wondering if there a formal proof for this:
Take any positive integer with
two or more digits. This is your first number, then shuffle the digits of that
integer to make your second number (so long as it is different from the first,
it doesn't how much you shuffle). Subtract the smaller number from the larger.
Sum the digits of the result. If the result is two digits, sum again and keep
doing that until the result is one digit. That final digit will be 9.
Example:
First number = 123.
Second number = 231.
Subtraction: 231-123 = 108.
Sum of digits (1): 1+0+8=9
Another example, with a number chosen at random (in
Excel):
First number: 202946140248026.
Second number (order randomised): 420292406506142.
Subtraction: 620294164428002 - 202946140248026 =
417348024179976.
Sum of digits (1): 4+1+7+3+4+8+0+2+4+1+7+9+9+7+6=72
Sum of digits (2): 7+2=9
---
My first thought was to generalise the problem by referring
to an arbitrary large, ordered set of digits (but note that it can be any integers),
A=[a1,…,ak].
Say also that there is another ordered set A', which contains the same
members as A, but in a different order.
Your first number would be given by:
And the second, which is an anagram of the first, by:
So the claim would resolve to this:
because, as we know and I will show shortly, any non-zero
multiple of 9 contains digits that sum to 9. Note that sometimes, the term "remainder" is used rather than "modulo" but all I am saying is that the number inside the large brackets is evenly divided by 9.
---
The procedure described above also works if you imagine a single
digit is buffered by an arbitrary number of zeroes (but at least one, so that
your second number is not the same as the first). Or you could start with any arbitrarily large
round number.
For example, say that we use 007 (licensed to thrill). Make
the second number 700. The result of subtraction is 693. Sum of digits(1)=6+9+3=18,
sum of digits(2)=1+8=9.
Adding more zeroes makes no difference, since each added
zero beyond the first simply adds a 9 in the subtraction result.
---
As I mentioned above, any integer that is evenly divisible
by 9 contains digits that sum to a number that is evenly divisible by 9. This is because any integer can be given by:
When i=1, we have (100-1)=0 and,
otherwise (10(i-1)-1) is a string of nines of length (i-1),
so that each product is evenly divisible by 9 and so too is the sum of the
products. More formally:
Thus an integer can be evenly divided by 9 if and only if
all its digits sum to a number that is evenly divisible by 9.
---
Note that neither the procedure nor the divisible by 9 proof
is limited to digits. It should be
reasonably obvious that, say, if we had three three-digit integers, say 987, 654 and 321, and ganged them together into one single
nine-digit, integer, 987654321, then subtracting a rearrangement of them that
keeps the three-digit integers together, say 321987654 is no
different to any other rearrangement in so far as the result being divisible by
nine goes.
The ganging together above is equivalent to summing 987×106, 654×103 and 321×100. A similar thing occurs if we use different
powers, say we sum 987×102, 654×101
and 321×100 and
subtract the summation of 321×102,
987×101 and 654×100. Because of buffering of zeroes, it doesn’t
even matter if the three digits are the same length. It also doesn’t matter whether powers are
organised in some logical way, or if they are the same between the first number
and the second number. So we could sum 987×108, 654×105 and 321×102
and subtract the summation of 321×104,
987×107 and 654×1011,
so long as the indices are whole (so that we don’t introduce roots) the result
is evenly divisible by 9.
Similarly, any combination integers ganged together, for
example 987, 654 and
321, will be evenly divisible by nine if the
sum of the instances of each integer amounts to a number that is evenly divisible
by 9. For example 321987321654321654321321321 is evenly divisible by 9, as 321+987+321+654+321+654+321+321+321=4221, which is evenly divisible by 9. The sum of the individual digits is 90, which
is evenly divisible by 9.
The same works if we resplit the final result into integers
that are seven and six digits long, so 3219873, 2165432, 1654321 and 321321. The sum of the integers is 7360947. The sum of the digits in that result is 36,
which is evenly divisible by 9.
---
This all hints at a proof.
As previously stated, any integer of length k can be
given by:
And we can describe any anagram of that integer as:
Since the second is the anagram of the first:
So:
Since:
Then:
Which implies that:
And thus that:
And so the difference between any integer and any non-identical
anagram of itself is evenly divisible by 9.
QED.
---
Does this count as a proof?
---
Note that there's a sort of magic prediction trick you can do with this, using words, but it's pretty much a once only affair. Write the number 9 somewhere and hide it, for example in a sealed envelope that you give your victim. Get the victim to select any word that has an anagram (for example "god" and "dog"). Write both down with sufficient space to write corresponding numbers for each letter underneath (a=1, b=2 and so on). Gang the resultant digits together to make two integers, so for god and dog, you will get 7154 and 4157. Subtract the smaller from the larger (in our example it would be 2997). Then keep summing the digits together until you have one number (so 2+9+9+7=27,2+7=9). Voilà!