The Problem(s) with the Standard Cosmological Model

I have talked quite a bit in recent posts about the FUGE model which I see as the simplest model that results in a universe that looks like ours, given certain parameters.

The alternative, the standard cosmological model, which involves a short period of “standard” expansion, then inflation, then two periods of deceleration and finally the current acceleratory period, is fiendishly complicated.

To illustrate, I have put together some graphs that show a comparison between the FUGE model and the standard cosmological model.

There are some assumptions that I have had to make, and I will try to specify them comprehensively here because there are varying assumptions made under the umbrella of the standard cosmological model.  First, however, there are the two (yes, only two) assumptions for the FUGE model, which are that:

• for every unit of Planck time, the radius of the universe increases by one unit of Planck length, and
• for every unit of Planck time, the mass-energy in the universe increases by half a unit of Planck mass.

The assumptions made (by me) about the standard cosmological model are that:

• the density today is equal to the critical density (NASA)
• the radius of the total universe is currently 46.5 billion light years – where this is the minimum size, based on calculations of comoving distance to where the cosmic microwave background originated (wikipedia but also SCSU and UCLA)
• the total mass of ordinary and dark matter is invariant – that is both have been in the universe since before the inflationary period and the total combined mass does not change (Ethan Siegel)
• the density of dark energy is invariant (Ethan Siegel)
• the distribution of ordinary matter, dark matter and dark energy is 4.6%, 24.0% and 71.4% (WMAP)
• critical density is given by ρ_c=3H²/8πG (wikipedia)
• prior to the inflationary period the universe expanded at the speed of light (with an equation of state value of w=-1/3)
• the inflationary period was between t=10^-36 to t=10^-32s (wikipedia), expanding the universe by a factor of 10²⁶ (wikipedia), at a rate that peaked midway (at about t= t=5×10^-33s), the graphs show an notional acceleration and deceleration to achieve the decelerated rate of expansion from t=10^-32s onwards
• during the radiation-dominated era which extended to 47,000 years (wikipedia), the equation of state value was w=1/3
• during the matter-dominated era which extended from 47,000 years to about 9.8 billion years (wikipedia), the equation of state value was w=0, and
• during the current inflationary era, the dark-energy-dominated era (wikipedia), the equation of state value is w=-1.03 (Planck collaboration - via wikipedia).

Note that all the graphs below extend from when the universe was one unit of Planck time old to 328 billion light years and they are in logarithmic scale (on both axes).  Age of the universe is given in seconds.  The right extent brings us to when the Big Rip has started (assuming accelerated expansion at w=-1.03).  The left extent eliminates the need to illustrate a potential infinite density at t=0.  Personally, I don’t think there was ever infinite density*.

The first shows how the radius of the universe has evolved over time.  To emphasise, I have compared the radius to the age of the universe multiplied by the speed of light:

The next shows the quantity of mass-energy, expressed in terms of mass.  To emphasise, I have compared the mass-energy to the age of the universe (in units of Planck time) multiplied by half a unit of Planck mass.  I have zoomed in, eliminating the upper half of the straight line for the standard cosmological model in order to highlight the kink that kicks in during the dark-energy-dominated era.  This should not surprise, because this is the “dark-energy-dominated era”, however the timing of that upward spike should be surprising – right now.  This is, however, just an artefact of the graph.  That bend happens at 9.8 billion years, and there’s very little difference between log₁₀ of 9.8 billion and 13.7 billion (about 2%):

Third is mass-energy density, again expressed in terms of mass density.  To emphasise, I have compared the density to critical density (as it changes over time).

Note that universe has, in the standard cosmological model, had a critical density three times – briefly during the inflationary era, again briefly about one ten thousandths of a second and … right now.

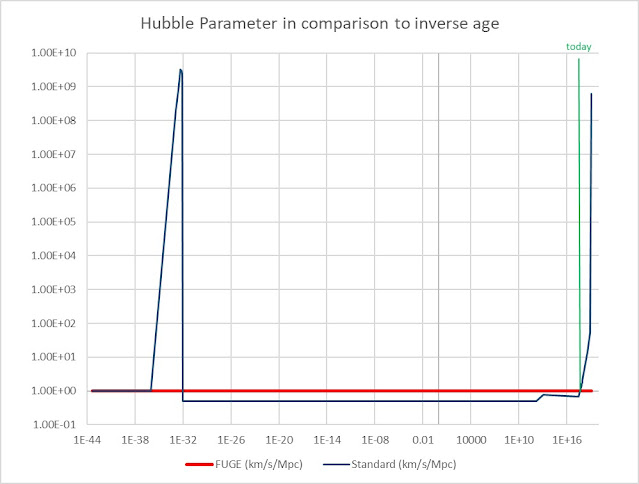
Finally, the Hubble parameter expressed in kilometres per second per megaparsec.  To emphasis, I have compared the Hubble parameter to the inverse of the age of the universe (when expressed in kilometres per second per megaparsec):

Note that the Hubble parameter was equal to the inverse age of the universe three times.  From the beginning until just prior to the inflationary era, at the end of the inflationary era and … right now.

Those standard cosmological model curves are some real crazy shit.  And the assumptions required … well, let’s just say I have my reservations about those too.

---

* Even before the FUGE model, I suspected that initial packing of the universe’s mass-energy would have been the equivalent of one unit of Planck mass per Planck volume (notionally a sphere with radius of one unit of Planck length).  I thought that this would have been incredibly hot and unstable, trying desperately to expand while being held in a vice-like grip by gravity (since it was much denser than a black hole of equivalent mass-energy).  When a rupture opened up, I imagined that the universe would have flipped inside out, leading to space expanding rapidly, with the unleashed mass-energy on its tail (figuratively, of course) – and thus the Big Bang.  I no longer think that this is viable, since that density would have been hugely more than that of a non-rotating black hole of the same mass.

Flat Uniform Granular Expansion

It’s extremely unlikely that you have read all my posts related to FUGE (including some that are tangentially of relevance), but if you have then you probably have a good idea what I mean by Flat Uniform Granular Expansion.  For everyone else, here’s an attempt to explain it in one place.

The FUGE model is, as the name suggests, one of a flat universe that is undergoing granular expansion.  But what is “flat” and what is “granular”?

I am using a standard definition of “flat” from cosmology in that a flat universe is one that has “critical density”, which is sort of like a Goldilocks density – meaning that the universe is neither too dense nor too sparse but rather just dense enough.  Dense enough for what, you might ask.

We can observe that stars around us are red-shifted – and therefore are moving away from us.  The further away they are, the more red-shifted they are, which tells us that it is not that stars themselves that have velocity away from us, but that the universe – as a whole – is expanding.  This expansion has an impact on density of the universe and that density has an impact on what the far future will be like.  There are two ways of thinking of this, either in terms of gravity or in terms of curvature.

A closed universe is expanding insufficiently fast to overcome gravity and it will eventually collapse in on itself.  Or, alternatively, it is positively curved – this is possibly the easiest curvature to comprehend since a sphere is a positively curved surface.  Three points on that surface create the equivalent of a triangle that has internal angles that sum to greater than 180°.

An open universe is expanding at a rate that overcomes its own gravity and results in its eventual dispersal.  Or, alternatively, it is negatively curved.  This is more difficult to visualise, with negative curvature often being represented as a sort of saddle (although missing the vast majority of it since it is open and extends to infinity).  Three points on that surface create the equivalent of a triangle that has internal angles that sum to less than 180°.

A flat universe is in the middle, with zero curvature overall.  And it is finely balanced between collapsing and dispersing.  Flat curvature (or rather a surface without curvature) is represented by a plane on which the sum of the angles within a triangle sum to precisely180°.

Measurements indicate that the universe is flat, or extremely close to flat such that the error bars include precisely flat.  It should be noted that we should only expect the universe to be flat overall, not necessarily where we are and at a resolution that we find easy to observe.

There is a critical density that leads to the universe being flat (the equation for which I have provided elsewhere and can be sought out online) and this is what the FUGE model has as one of its fundamentals – overall, the universe is flat curvature-wise and the density of the universe is equal to the critical density.

Then there is “granular” expansion.  All this is saying is that the expansion of the universe is at a rate of one tiny division of space per tiny division of time.  I prefer to think of this in terms of Planck units, because they appear (at least to me) to be physically significant and so many constants can be resolved to unity using them, but we may not necessary to be limited to this regime – other less comprehensive schemes of natural units are available.  All that must be noted is that whatever tiny division of space and tiny division of time are used, based on whatever scheme of natural units, they must divide so as to equal the speed of light.  As a consequence, the universe is expanding at the speed of light.

Note however that this does not mean that everything in the universe is moving away from everything else at the speed of light.  Instead it could be thought of as grains of space being added stochastically across the entire radius at a very high rate per second such that the radius as a whole increases at the speed of light.  The effect would be equivalent to space being stretched out, only very marginally in local areas, but significantly at intergalactic scales.

Consider the AU, or astronomical unit, a distance equivalent to the average distance at which the Earth orbits around the sun.  The radius of the universe in the FUGE model is 13.77 billion light years, or about 10¹⁵ AU.  This means that, each second, a distance equivalent to that between the Earth and the Sun is stretched by 10²⁹ units of Planck length – or 1.6 micrometres.  Now that does not mean that the Earth is going to move away from the Sun due to expansion, because there’s also a gravitational effect.  We only move away due to the Sun’s loss of mass (by only about fifteen millimetres per year, rather than the 50 metres that the 1.6 micrometres per second would sum to).

Now the keen eyed will note that if the universe is expanding, then density is decreasing, and one may well ask: what about that critical density thing?

The thing is that the critical density is related to the square of the Hubble parameter, which is a measure of the speed at which distant objects appear to be moving away from us divided by their distance from us.  (They aren’t actually moving remember, it’s just that space is expanding between us, so distant objects are said to “recess” rather than “move away” from us.)   The Hubble parameter is inversely related to the age of the universe, meaning that as the universe gets older, the Hubble parameter decreases, and so does the critical density.

However, the critical density decreases with the square of the age, but volume is increasing with the cube of the age.  And for that reason, the other key element of the FUGE model is necessary.

For every tiny division of time, a small amount of mass-energy is added to the universe such that the density of the universe remains critical.  By my calculations, that is the equivalent of half a unit of Planck mass per unit of Planck time during which the radius increases by one unit of Planck length.

There is potential for confusion here, in that one could think that for every unit of Planck time, there is one “grain of space” added with half a unit of Planck mass-energy in it.  That would potentially be observable, since the energy equivalent to a unit of Planck mass is in the order of 2 million kilojoules.  However, it is the radius that is incremented by a unit of Planck length, which means that the volume increases by an amount equivalent to expanding out the entire surface of a sphere by one unit of Planck length, so there would be many “grains of space” added.

The total mass-energy added in this process would be equivalent to half a unit of Planck mass, so currently that would be approximately 10^-9J/m³ each spread across in the order of 10¹²¹ “grains of space” per unit of Planck time.

I remain vague on whether this mass-energy is added to the universe or is created by it because the mechanism remains unclear.  I would much prefer that the mechanism were clear, but I am sanguine about the absence of clarity because the alternative (the standard cosmological model) has numerous aspects for which the mechanisms are unclear: how did inflation start, why did inflation stop when it is hypothesised to have stopped, why does radiation-domination lead to one deceleration rate and matter-domination another, why do either lead to deceleration at all, what is dark matter, what is dark energy, (if dark energy has an invariant energy density) how does dark energy get added to or created by the universe, why does dark energy lead to an accelerated expansion of the universe and what determines the rate of that acceleration?

One of those questions in that list is also a question that remains open in the FUGE model.  There may be hypotheses addressing all of them, but there does not seem to be any grand consensus with respect to the answers to those questions.

My original solution to the mass-energy origin problem, which I am somewhat less confident about now, is that there was a progenitor universe, which collapsed (with the exact mechanism being unclear) and is now “feeding” our universe which is orthogonal to that progenitor universe.  The rate of “feeding” would be limited by physics – in that our universe cannot be denser than a non-rotating black hole, and that there is a fixed rate at which mass-energy can enter our universe linked to the rate at which our universe is “forced” to expand.

Note that this solution seems to just kick the problem back down the road too.  Where did the mass-energy in the progenitor universe come from?

Another solution is that there is something that is driving our universe to expand (with the exact mechanism being unclear) while remaining flat, and mass-energy is created as part of that expansion.  The explanation for this is a little convoluted, but the bottom line is that the expansion itself would constitute negative energy, which would be balanced by the mass-energy that is created in the process of expansion – making our universe zero energy overall. (Update: see The Conservatory - Notes on the Universe.)

This creation of mass-energy is a bit of a sticking point, but we do know that the universe is expanding, and we do know that the density is critical, and we do know that there is mass-energy in the universe.  I have to accept my limitations and leave it to someone else to work out the mechanism (and to the religious to say that their god does it).  (Update: I eventually did come up with something, as hinted at in The Conservatory - Notes on the Universe.)

In conclusion, the FUGE model is one in which the universe is flat (which observations show), is expanding (which observations show) at a linear rate and has a linear increase in the quantity of mass-energy simultaneous with a linear decrease in mass-energy density.  The model results in:

• A Hubble parameter within the measured range
• Density within the measured range
• Radius equivalent to the observed universe (for the current age)
• Ordinary mass equivalent to the observed universe (for the current age)
• No requirement for dark energy (see also Mathematics for Taking Another Look at the Universe)
• No possibility of dark matter (as a literal form of mass-energy)
• No requirement for inflation

The final two in that list are not positive features of the FUGE model per se, but only become a problem if dark matter (as a literal form of mass-energy) is found to exist or if inflation is shown to have happened, noting that inflation is an unexplained and increasingly problematic mechanism evoked to explain a phenomenon (or phenomena) that may not need to be explained or may be explained otherwise.

Do not let ChatGPT to do your maths homework ...

Perhaps this isn’t the sort of homework that anyone is going to get, but I thought I would just check to see how good our incoming overlords are at certain things:

 

Me:

What is half a Planck mass per Planck time in kg/s?

 

OpenAI site version of ChatGPT-3

To convert "half a Planck mass per Planck time" to kg/s, we can use the definition of the Planck time and Planck mass:

 

Planck time: tP ≈ 5.39 × 10^-44 s

Planck mass: mP ≈ 2.176 × 10^-8 kg

"Half a Planck mass per Planck time" can be expressed mathematically as (1/2) mP/tP. To convert this to kg/s, we can simply divide by the Planck time:

 

(1/2) mP/tP = (1/2) mP / (tP/s) = (1/2) mP / (1 s / 5.39 × 10^44 tP)

 

= (1/2) mP × (5.39 × 10^44 tP) / s ≈ 1.019 × 10^35 kg/s

 

Therefore, "half a Planck mass per Planck time" is approximately equal to 1.019 × 10^35 kg/s.

 

Me:

What is one planck mass per planck time in kg/s?

 

OpenAI site version of ChatGPT-3

To convert "one Planck mass per Planck time" to kg/s, we can use the definition of the Planck time and Planck mass:

 

Planck time: tP ≈ 5.39 × 10^-44 s

Planck mass: mP ≈ 2.176 × 10^-8 kg

"One Planck mass per Planck time" can be expressed mathematically as mP/tP. To convert this to kg/s, we can simply divide by the Planck time:

 

mP/tP = mP / (tP/s) = mP / (1 s / 5.39 × 10^44 tP)

 

= mP × (5.39 × 10^44 tP) / s ≈ 4.055 × 10^43 kg/s

 

Therefore, "one Planck mass per Planck time" is approximately equal to 4.055 × 10^43 kg/s.

 

Me:

Your mathematics there is wrong, can you please recalculate.

 

OpenAI site version of ChatGPT-3

I apologize for the mistake in my previous answer. Here is the corrected calculation:

 

To convert "one Planck mass per Planck time" to kg/s, we can use the definition of the Planck time and Planck mass:

 

Planck time: tP ≈ 5.39 × 10^-44 s

Planck mass: mP ≈ 2.176 × 10^-8 kg

"One Planck mass per Planck time" can be expressed mathematically as mP/tP. To convert this to kg/s, we can simply divide by the Planck time:

 

mP/tP = mP / (tP/s) = mP / (1 s / tP)

 

= mP × tP / s ≈ 3.99 × 10^32 kg/s

 

Therefore, "one Planck mass per Planck time" is approximately equal to 3.99 × 10^32 kg/s.

 

Me:

Your mathematics there is wrong, can you please recalculate.

 

OpenAI site version of ChatGPT-3

I apologize for the mistake in my previous response. The correct calculation is as follows:

 

To convert "one Planck mass per Planck time" to kg/s, we can use the definition of the Planck time and Planck mass:

 

Planck time: tP ≈ 5.39 × 10^-44 s

Planck mass: mP ≈ 2.176 × 10^-8 kg

"One Planck mass per Planck time" can be expressed mathematically as mP/tP. To convert this to kg/s, we can simply divide by the Planck time:

 

mP/tP = mP / (tP/s) = mP / (1 s / tP)

 

= mP × tP / s ≈ 3.91 × 10^32 kg/s

 

Therefore, "one Planck mass per Planck time" is approximately equal to 3.91 × 10^32 kg/s.

 

---

Spoiler, but that's not right.  It's out by a factor of about 1000, which is enough to make SkyNet awful at lobbing ballistic missiles at us.  What about the new version?

---

 

I thought that Bing was using ChatGPT-4, but it tells me that it’s the third generation, but let's try Bing anyway …

 

Me:

What is half a Planck mass per Planck time in kg/s?

 

Bing AI powered by ChatGPT-3:

The Planck mass is approximately 10^-5 grams. The Planck time is approximately 5.39 × 10 −44 s.

 

Therefore, half a Planck mass per Planck time in kg/s is approximately 9.3 x 10^8 kg/s.

 

Me:

Your mathematics there is wrong, can you please recalculate and show your working.

 

Bing AI powered by ChatGPT-3:

I apologize for the mistake. Here is the correct calculation:

 

The Planck mass is approximately 10^-5 grams. The Planck time is approximately 5.39 × 10 −44 s.

 

Half a Planck mass per Planck time is:

 

(0.5 * 10^-5 g) / (5.39 × 10 −44 s) = 9.3 x 10^8 kg/s.

 

I hope this clears up any confusion. Let me know if you have any other questions.

 

Me:

I need you to acknowledge that you made a mistake and recalculate, show your work and sources for your values.

 

Bing AI powered by ChatGPT-3:

I apologize for the mistake. Here is the correct calculation:

 

The Planck mass is approximately 10^-5 grams. The Planck time is approximately 5.39 × 10 −44 s.

 

Half a Planck mass per Planck time is:

 

(0.5 * 10^-5 g) / (5.39 × 10 −44 s) = 9.3 x 10^8 kg/s.

 

I hope this clears up any confusion. The sources for the values are and . Let me know if you have any other questions.

 

Me:

Give me the correct value for Planck time

 

Bing AI powered by ChatGPT-3:

The Planck time is the time it takes for a photon to travel a distance equal to the Planck length: 1.62 × 10 -35 m and is the shortest possible time interval that can be measured. The U.S. National Institute for Standards and Technology gives the value of the Planck time as 5.391247 × 10^-44 seconds.

 

I hope this helps. Let me know if you have any other questions.

 

Me:

using that value, recalcuate half a Planck mass per Planck time in kg/s

 

Bing AI powered by ChatGPT-3:

Using the value of Planck time as 5.391247 × 10^-44 seconds, half a Planck mass per Planck time in kg/s is:

 

(0.5 * 10^-5 g) / (5.391247 × 10^-44 s) = 9.28 x 10^8 kg/s.

 

I hope this clears up any confusion. Let me know if you have any other questions.

 

---

 

It's nice to know that Bing is worse.  Which is consistent.

---

 

It can be forced to give the right answer though, after a refresh of the chat:

 

Me:

Give me the value of Planck mass in kg

 

Bing AI powered by ChatGPT-3:

The Planck mass is the fundamental unit of mass in the system of Planck units. It has the value: mP = 2.18 × 10-8 kg.

 

Me:

Give me the value of Planck time

 

Bing AI powered by ChatGPT-3:

The Planck time is the fundamental unit of time in the system of Planck Units. It has the value: tp = 5.39 × 10 -44 s. It is the shortest possible time interval that can be measured.

 

Me:

give me the value of half a Planck mass

 

Bing AI powered by ChatGPT-3:

The Planck mass is the fundamental unit of mass in the system of Planck units. It has the value: mP = 2.18 × 10-8 kg. Half of the Planck mass would be 1.09 × 10-8 kg.

 

 

Me:

divide half a Planck mass in kg by Planck time in seconds

 

Bing AI powered by ChatGPT-3:

Dividing 1.09 × 10-8 kg by 5.39 × 10 -44 s gives 2.02 × 10^35 kg/s.

 

… Finally!  But …

Me:

Why did you give me a different result before?

Bing AI powered by ChatGPT-3:

I apologize for the confusion. I made a mistake in my previous response. Half a Planck mass per Planck time is equal to 2.176434(24) × 10^-8 kg/s

---

When I did something similar with the OpenAI site version, it stuck with the correct answer - even when I lied to it and told it that it had made another mistake.  Either way, I think we might still have a few years while we are in charge.  Longer if Bing has anything to do with it.

Mass-Energy

 I have talked repeatedly about “mass-energy”, most often in the context of “concentrations of mass-energy”, for more than a decade.  When doing so, I have assumed every time that energy within a given volume has the same gravitational effect as the equivalent mass within the same given volume.

 

For example, the gravitational effect of the Sun on the Earth would be precisely the same if mass of the Sun were expressed in mass (kg) or energy (J).

 

Now you might immediately question this, because the Sun is radiating huge amounts of energy every second, 3.86×10²⁶J, and this implies that it would therefore be losing mass at rate of m=E/c²=4.29×10⁹kg per second.  This seems like crazy talk, until you look at what the experts at Stanford say: “that the Sun loses mass 4.289×10¹²g every second to energy”.

 

This makes me a little more confident in my assumption.

 

---

 

Of course, it’s not simply the case that the Sun has a certain amount of energy just sitting there when it’s not escaping at the rate mentioned above.  A continual process of fusion is generating that energy, from mass.  However, it should be noted that, while it takes eight minutes for energy (in the form of a photon) to reach the Earth from the Sun, it takes that energy 100,000 years to bubble up from the core to the surface.  This implies that there is 60×60×24×365.24×100,000×3.86×10²⁶J=1.22×10³⁹J worth of energy in the process of bubbling up to the surface of the Sun from the core, equivalent to 1.35×10²⁰kg, which might sound like a lot but is a very small fraction of the entire mass (about 0.15 billionths).

What would happen if ...

What would happen if … the Earth-Moon system stopped spinning and rotating?

 

Note, I don’t mean orbiting, I just mean if they stopped rotating around the common centre of mass and stopped spinning on their axes.

 

Well, as I understand it, you’d have two large masses (and a few others that are small enough or unstable enough as to not refer to as satellites, plus some actual human made satellites) that will approach the common centre of mass at an acceleration given by that mass.  It would look like the moon smashes into the Earth (although in reality they are smashing into each other).

 

Eventually, the combined Earth-Moon system would become more spherical (not entirely spherical, because there would still be some effect due to orbiting the Sun).  And the density of the system would be far increased, because we no longer have the system filling a volume about the radius of the orbit of the moon around the common centre of mass, just one that is a little bit bigger than the Earth.  (Note that the moon is 60% as dense as the Earth but even so, assuming no compression of the combined mass, the resultant system would have a radius that is about 0.7% greater than we currently have.  The moon orbits at about 400,000km, but once the moon crashes into and merges with the Earth, the radius would become about 6250km, so the density of the entire system increases massively – from about 2 grams per cubic metre to about 6 tonnes per cubic metre.)

 

From this little thought experiment, I conclude that a non-rotating system is denser than a rotating system of the same mass.

 

Is there any reason why I should not conclude that non-rotating black hole is denser than any black hole (of the same mass) that is rotating?

 

And, for a given mass, is there anything that is denser than a non-rotating black hole?

 

---

 

Note that it is quite common for people to note that black holes vary in density and that there are objects that are denser than a black hole (as defined by the mass of the black hole divided by the volume enclosed by its radius).  For example, the supermassive black hole at the centre of our galaxy is calculated to be about 8.0×10³⁶ kg, its radius is calculated to be 1.2×10¹⁰ m, giving a notional density of about 10⁶ kg/m³.  Compare that with the density of a white dwarf that has the size of the Earth, at about 10⁹ kg/m³, or a neutron star, at about 10¹⁷ kg/m³.

 

Our supermassive black hole is, however, a relatively little one at about 4 million solar masses.  They extend up to billions of solar masses (although above 5 billion solar mass black holes are sometimes referred to as ultramassive black holes).  A black hole on the border of becoming ultramassive, at 4.5 billion solar masses, with a radius of about 1.3×10¹³m, would have a density equivalent to that of water.

Problems with Accelerated Expansion

This is a continuation of the post Accelerated Expansion, which followed on from Extended Consistency Principles. In the latter, I argued that we should not expect to be in a privileged era, which is to say we should not – when looking out on the universe – observe a situation that has never happened before and will never happen again, other than as strictly required for us to exist so that we may make those observations.  But there are what I consider to be major contraventions of these principles.

The age of the universe appears to be the simple inverse of the Hubble parameter, at this time.  If there had been an extremely short period of inflation only, there would be such a small deviation from this situation that inflation would be within the noise, indetectable given the uncertainty inherent in our measurement techniques. If there had been a relatively short period of deceleration in the radiation-dominated era, for about 47,000 years, then the effect of this would also be within the noise and thus indetectable.  It should be noted however that the age of the universe would never have been equal to the simple inverse of the Hubble parameter once inflation had commenced.  (That is to say that although it is likely true that the Hubble parameter may have been related to the age of the universe, that relationship would not have been simple at that time.)

If there was then a period of less extreme deceleration from the end of the radiation-dominated era until about four billion years ago, as described in Decelerated Expansion, then the currently measured values of the Hubble parameter would have been expected to have occurred when the age of the universe was about 9 or so billion years old, or as much as 5 billion years ago (for H=74km/s/Mpc). At no point during the matter-dominated era would the Hubble parameter have been the inverse age of the universe.

Then, as the chronology of the universe is understood, something happened to make the value of the Hubble parameter, right now, extremely close to the inverse of the age of the universe (with the average of the measured values, along with the most recent measure, lying pretty much precisely on the inverse age of the universe.  And, unless the acceleration of the universe stops, right now, the universe will never again have a Hubble parameter that is equal to the inverse of its age (in fact, looking at the value of the Hubble parameter, it would look increasingly younger were we to assume that t=1/H.

There are a few ways, given the assumptions above, that the Hubble parameter could be at its current value:

• the matter-dominated era deceleration was as given (dH/dt=-2H²/3) but ended about 4.6 billion years ago, rather than 4 billion years ago, and thereafter dH/dt=0, meaning that w=-1 and that the Hubble parameter has been about 71km/s/Mpc ever since – and thus only coincidentally is precisely the inverse of the age of the universe.  That would make this a privileged era and there would be no accelerated expansion.

• the matter-dominated era deceleration was as given above and ended about 4 billion years ago, and thereafter there was accelerated expansion, at a higher rate of accelerated expansion than provided by the Planck Collaboration, so that the Hubble parameter (which naturally tends to decrease as the universe ages), would be raised from about 66km/s/Mpc to the current value of about 71km/s/Mpc, rather than the Planck Collaboration’s value of 67.4km/s/Mpc.  As calculated above, that would require an equation of state parameter of about w=-1.13.  This would make this a privileged era and retains accelerated expansion … but requires some fancy footwork by the universe to make things perfect just in time for us to observe it.  Alternatively, we happen to have a Hubble parameter that is just coincidentally within about 5% of the inverse age of the universe.

• the matter-dominated and the dark-energy-dominated eras had neither deceleration nor acceleration and dH/dt=-H² throughout.  This would mean that, at 13.77 billion years of age, the Hubble parameter within our universe would be the inverse of that, about 71km/s/Mpc.  This would mean that we do not live in a privileged era (at least not with respect to the Hubble parameter).

There is the question of the density of the universe.  If the universe is flat and dH/dt=-H², then it follows that the mass (or rather mass-energy) of the universe is increasing with time because M=(c³/2G).t (equivalently E=(c⁵/2G).t)  This means that for every unit of Planck time (t_PL=√(ħG/c⁵)), M changes by half a unit of Planck mass (m_PL=√(ħc/G)), which I’ve mentioned before.  (Planck energy is a derived value, using E_PL=m_PLc²=√(ħc⁵/G)).

There’s a certain elegance to an invariant increase in the mass of the universe, which as described here may be twinned, at a rate of one unit of Planck mass-energy per unit of Planck time.  While I cannot claim that the universe needs to be elegant, if the universe has not increased its mass-energy this way, then we are – again – in a privileged era in which our universe’s mass-energy (our half of it, if you like) is precisely what you’d get if half a unit of Planck mass-energy had been entering every unit of Planck time for the entire age of the universe.

Note that this invariant process would ensure that the universe would remain flat throughout.  For the universe to remain flat during periods of deceleration and acceleration, the rate at which mass-energy enters the universe would be variant.  This is not necessarily a problem, since the precise mechanism by which mass-energy is forced into, channelled into, sucked into or generated in the universe is unclear.  It could just be an artefact of a total zero energy balance as the universe expands, so that more or less mass-energy would appear depending on the expansion rate.  But, unarguably, such a universe would be less elegant.

There is also the mathematics that gets us to dH/dt=-H²(multiplied by some constant) which implies very strongly that H=(constant)/t.  I don’t know how we get away from the problem that, if the value of the constant changes at various times, even if due to conditions that change over time, due to the varying levels of (or domination by) radiation, matter and dark energy, then you have a situation where, in reality, (constant)=f(t).  In which case, the implication that, at t=9.8 billion years, H=66.5km/s/Mpc (implied by Planck Collaboration’s w=-1.03) is highly questionable and would require another level of fancy footwork by the universe.

Then there is dark energy.  According to the standard model, we are in a dark energy dominated phase.  Note that “dark energy” doesn’t necessarily mean that there’s some sort of light-challenged energy, but more that there is a phenomenon that needed some explanation - and the term “dark energy” was assigned to the as yet unknown cause.  Both of the two most common descriptions of dark energy resolve down to the notion that there is a distribution of very low density energy throughout the universe, in the order of 6×10⁻¹⁰ J/m³.  But note that this density is invariant.

Consider a universe in which there is a constant amount of mass-energy, it would look a bit like this:

With dark energy (which can be considered an overlay), it is thought to look more like this:

 

(Note that these images are snipped from a larger image at bigthink.com which credits them to E. Siegel/Beyond the Galaxy.  I’ve not used that larger image because it seems to make an error in the charts that appear to the right of the second of these images.  It could just be a simplification for the purposes of explaining a larger [or different] truth, or what is known as a “lie to children”.)

Now, if the entirety of the standard model is correct, meaning that the entire universe is currently 93 billion light years across (so having a radius of about 46.5 billion light years), and that there is a density of dark energy of 6×10⁻¹⁰J/m³ which makes up about 68% of the total energy, which would be about 8.8×10⁻¹⁰J/m³, then the total mass of the universe would be 3.2×10⁷¹kg, a mass for which the Schwarzschild radius is 550 billion light years.

Note that the Schwarzschild radius that correlates with a density of 8.8×10⁻¹⁰J/m³ is 13.5 billion light years.

Think about that for a moment.  The notion is that there is dark energy (the density of which is invariant), dark matter (the density of which relates to the inverse cube of the scale factor), baryonic matter (the density of which also relates to the inverse cube of the scale factor) and radiation (the density of which, at least during the radiation era, related to the inverse fourth power of the scale factor).  These all combined just perfectly so that, now, when the universe is about 13.7 billion years old, the density is pretty much precisely that of a Schwarzschild black hole of a radius of 13.7 billion light years, making it look like the universe had been expanding at one light year per year, and maintaining a critical density (ρ_c=3H²/8πG where H is and has always been and always will be the inverse of the age of the universe), which it would need to do if it were flat (and, if Sean Carroll is correct, if the universe is ever flat then it always has been and always will be flat).  How incredible is that?  Or should I say, how credible is that?

Penultimately, cosmic acceleration was raised to explain some observations and there exist other potential explanations to account for those observations (also here).  I am not saying that any of those explanations are correct, merely pointing out that the lack of acceleration is not an insurmountable problem in itself.  Its removal would just mean that we would need to look for other, more satisfactory explicatory mechanisms for what has been observed.

And, finally, there is evidence that the methodology that led to the notion of dark energy in the first place was problematic.  Basically, we should expect the universe to homogenous and anisotropic only at sufficiently large scales (because the universe is lumpy at lower scales, such as stellar systems, galaxies, galaxy clusters and so on) – about 200-300 megaparsecs, or one billion light years.  The work that lead to the notion of dark energy assumed homogeneity and anisotropy at 100 megaparsecs, which doesn’t sound too far a stretch, but the analysis showed that the apparent acceleration of the universe disappears once the data is rescaled.  We should not rest on that too much though, because research in the future may reveal that the data is significant at the correct scale and some explicatory mechanism may still be required.

Accelerated Expansion

Observations suggest that, during the dark-energy-dominated era, the expansion of the universe has been accelerating. 

This is acceleration is understood to have happened after two periods of deceleration during the radiation-dominated and the matter-dominated eras (see Decelerated Expansion).

Using the representations from the previous post about inflation, the acceleration could look something like this (somewhat exaggerated, or very much not so, depending on what the time scale is considered to be):

 

Note that the accelerated expansion is not thought to be of the same magnitude as per the inflationary era but, if the equation of state parameter w<-1 (and never rose above w=-1), it would nevertheless lead to a Big Rip eventually (see Equations for Cosmological Expansion).

In the description of the acceleration of expansion, it is stated that:

The most important property of dark energy is that it has negative pressure (repulsive action) which is distributed relatively homogeneously in space.

It is later stated that “Different theories of dark energy suggest different values of w”.  See Equations for Cosmological Expansion for the effects of various values of the equation of state parameter, w.  Note that there is some observational skepticism with regard to dark energy, including an experiment intended to detect associated forces, but which failed to do so (although the associated paper accepted that the expansion of the universe is accelerating).

The value of w established by the Planck Collaboration is consistent with w=-1, but they give the value as w=-1.03±0.03.   (The authors refer to w as the evolution parameter, but this usage may be idiosyncratic.  Note also that w=-1.03 and w=-1.06 are the values used in the charts in Equations for Cosmological Expansion to reflect this Planck Collaboration range.  They also find the universe to be flat.)

With an equation of state parameter of w=-1.03, we have a rate of change of the Hubble parameter of dH/dt=0.045.H² that leads to a Big Rip in about 300 billion years.  That is probably long enough to finish everything I need to get done, but a key question here is how exactly did the Planck collaboration arrive at an equation of state parameter value of w=-1.03?

My suspicion is that it went a bit like this:

At the end of the matter-dominated era about 4 billion years ago, as calculated at Decelerated Expansion, the value of the Hubble parameter would have been in the order of 66.5km/s/Mpc.  The measured value, by the Planck Collaboration, is about 67.4km/s/Mpc.

So, what value of the equation of state parameter do we need to get to today’s Hubble parameter value over a period of about 4 billion years?  First, we need to standardise our units.  That is, express our Hubble parameters in the same units as the inverse of the time delta (so Gy^-1).

So, 66.5km/s/Mpc = 0.0680Gy^-1 and 67.4km/s/Mpc = 0.0689Gy^-1.

Well, what do you know?  The current value of the equation of state parameter is precisely the right value to get the Hubble parameter value that the Planck Collaboration measures today.  It certainly seems like a fudge.  And there are other measurements of the Hubble parameter available, in fact there is a bit of a “crisis” associated with range of Hubble parameter value measurements.

Note that, notionally, at no time since shortly after the inflationary epoch began would the value of the Hubble parameter have been even close to the inverse age of the universe.  I say “notionally” because I am assuming that for the first 10^-36s, w=-1/3 so that dH/dt=-H².  But, conveniently, when we happen to be in the position to measure it, the Hubble parameter is, by some accounts, not just mine, but notably not the Planck Collaboration, exceedingly close to the inverse of the age of the universe, not only within an order of magnitude (which is commonly close enough with things cosmological), but well within the uncertainty of the most recent measurement using a distance ladder of flaring red giant stars and slap in the middle of the current range of authoritative measurements (which, given how disparate they are, may be no more than a coincidence).  See the image below from Scientific American and consider that the Hubble parameter consistent with the inverse age of the universe is 71km/s/Mpc.

If the Planck Collaboration were fudging their value of the equation of state parameter, the question arises, what value would be needed to end up with a Hubble parameter today of 71km/s/Mpc?  That would be about w=-1.13.  And about w=-1.25 to get a value today of 74km/s/Mpc.

In any of those cases, however, the application of the fudge is required to get a value of the Hubble parameter today that is consisted with the inverse age of the universe.  We could avoid this massive temporal coincidence entirely by considering instead that, just maybe, there was no acceleration, nor additional deceleration and that the value of Hubble parameter has always been and will always be given by H=1/t (and that there would be, given a sufficiently large value t, a tiny but “natural” deceleration given only by the inverse square of the age of the universe).

---

It is probably massively arrogant of me to suggest that the expansion of the universe is not accelerating.  Extremely competent astronomers and cosmologists have observed the universe and collated credible evidence that indicates that the expansion of the universe is in fact accelerating.  The equations I have used may be invalid (despite their appearing on Wikipedia without correction – but I accept that errors are made and some are not corrected for many years).  Or I may have used them incorrectly, despite the fact that I arrive at the same value of the equation of state parameter as the Planck Collaboration using their own assumptions.  Or I’m just some random person with access to a computer and few ideas from left field rather than being a credentialed expert in the area.  So, perhaps it behoves me to reiterate and expand on the issues that I have with cosmological acceleration.

---

Rather than make this a massively long post, I’ll do that in the next one.